Learning the Sampling Pattern for MRI

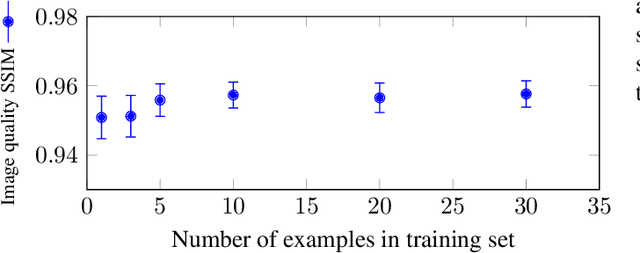
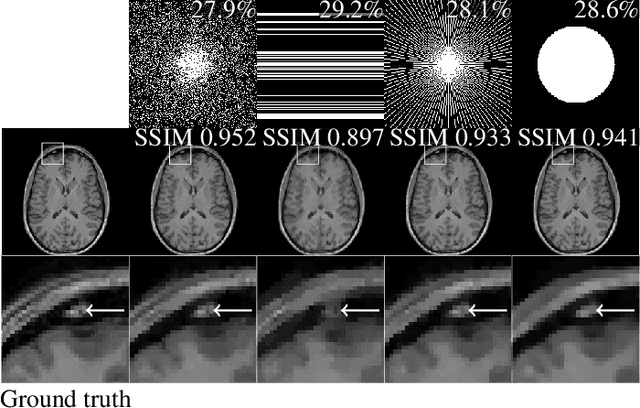
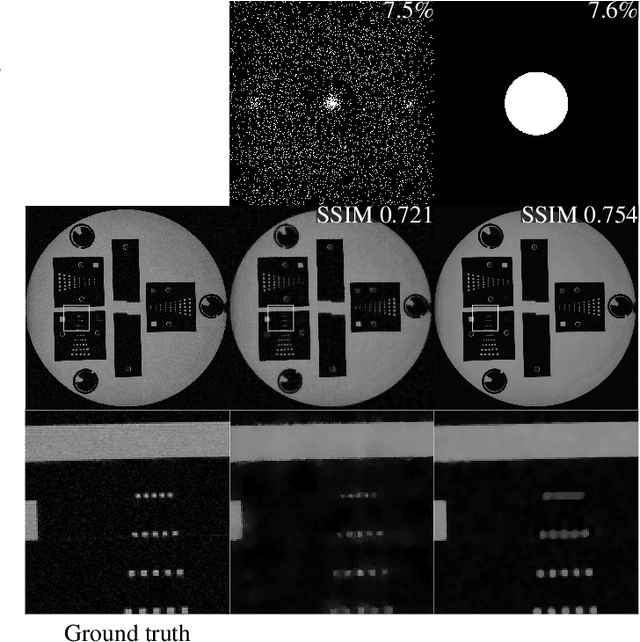
The discovery of the theory of compressed sensing brought the realisation that many inverse problems can be solved even when measurements are "incomplete". This is particularly interesting in magnetic resonance imaging (MRI), where long acquisition times can limit its use. In this work, we consider the problem of learning a sparse sampling pattern that can be used to optimally balance acquisition time versus quality of the reconstructed image. We use a supervised learning approach, making the assumption that our training data is representative enough of new data acquisitions. We demonstrate that this is indeed the case, even if the training data consists of just 5 training pairs of measurements and ground-truth images; with a training set of brain images of size 192 by 192, for instance, one of the learned patterns samples only 32% of k-space, however results in reconstructions with mean SSIM 0.956 on a test set of similar images. The proposed framework is general enough to learn arbitrary sampling patterns, including common patterns such as Cartesian, spiral and radial sampling.

Compressed Sensing Plus Motion (CS+M): A New Perspective for Improving Undersampled MR Image Reconstruction

Purpose: To obtain high-quality reconstructions from highly undersampled dynamic MRI data with the goal of reducing the acquisition time and towards improving physicians' outcome in clinical practice in a range of clinical applications. Theory and Methods: In dynamic MRI scans, the interaction between the target structure and the physical motion affects the acquired measurements. We exploit the strong repercussion of motion in MRI by proposing a variational framework - called Compressed Sensing Plus Motion (CS+M) - that links in a single model, simultaneously and explicitly, the computation of the algorithmic MRI reconstruction and the physical motion. Most precisely, we recast the image reconstruction and motion estimation problems as a single optimisation problem that is solved, iteratively, by breaking it up into two more computationally tractable problems. The potentials and generalisation capabilities of our approach are demonstrated in different clinical applications including cardiac cine, cardiac perfusion and brain perfusion imaging. Results: The proposed scheme reduces blurring artefacts and preserves the target shape and fine details whilst observing the lowest reconstruction error under highly undersampling up to 12x. This results in lower residual aliasing artefacts than the compared reconstructions algorithms. Overall, the results coming from our scheme exhibit more stable behaviour and generate a reconstruction closer to the gold-standard. Conclusion: We show that incorporating physical motion to the CS computation yields a significant improvement of the MR image reconstruction, that in fact, is closer to the gold-standard. This translates to higher reconstruction quality whilst requiring less measurements.