Bilevel Imaging Learning Problems as Mathematical Programs with Complementarity Constraints

We investigate a family of bilevel imaging learning problems where the lower-level instance corresponds to a convex variational model involving first- and second-order nonsmooth regularizers. By using geometric properties of the primal-dual reformulation of the lower-level problem and introducing suitable changes of variables, we are able to reformulate the original bilevel problems as Mathematical Programs with Complementarity Constraints (MPCC). For the latter, we prove tight constraint qualification conditions (MPCC-MFCQ and partial MPCC-LICQ) and derive Mordukovich (M-) and Strong (S-) stationarity conditions. The S-stationarity system for the MPCC turns also into S-stationarity conditions for the original formulation. Second-order sufficient optimality conditions are derived as well. The proposed reformulation may be extended to problems in function spaces, leading to MPCC's with additional constraints on the gradient of the state. Finally, we report on some numerical results obtained by using the proposed MPCC reformulations together with available large-scale nonlinear programming solvers.

Learning the Sampling Pattern for MRI

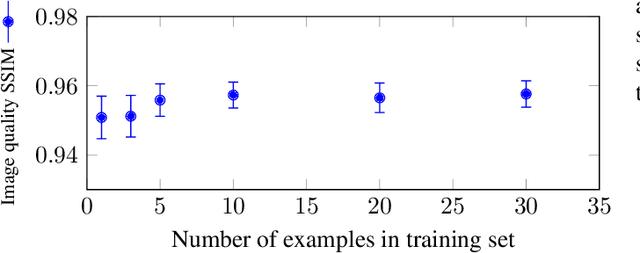
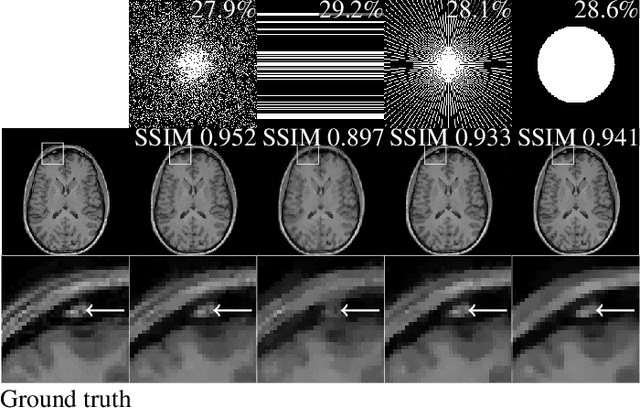
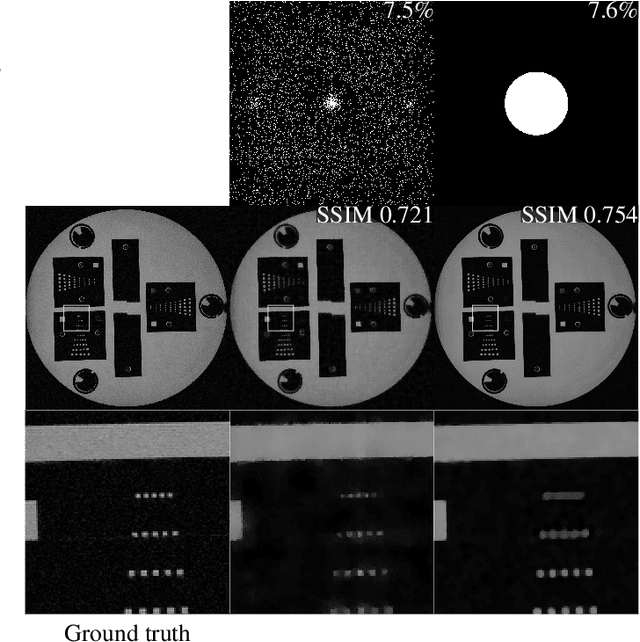
The discovery of the theory of compressed sensing brought the realisation that many inverse problems can be solved even when measurements are "incomplete". This is particularly interesting in magnetic resonance imaging (MRI), where long acquisition times can limit its use. In this work, we consider the problem of learning a sparse sampling pattern that can be used to optimally balance acquisition time versus quality of the reconstructed image. We use a supervised learning approach, making the assumption that our training data is representative enough of new data acquisitions. We demonstrate that this is indeed the case, even if the training data consists of just 5 training pairs of measurements and ground-truth images; with a training set of brain images of size 192 by 192, for instance, one of the learned patterns samples only 32% of k-space, however results in reconstructions with mean SSIM 0.956 on a test set of similar images. The proposed framework is general enough to learn arbitrary sampling patterns, including common patterns such as Cartesian, spiral and radial sampling.