Modelling Global Trade with Optimal Transport

Global trade is shaped by a complex mix of factors beyond supply and demand, including tangible variables like transport costs and tariffs, as well as less quantifiable influences such as political and economic relations. Traditionally, economists model trade using gravity models, which rely on explicit covariates but often struggle to capture these subtler drivers of trade. In this work, we employ optimal transport and a deep neural network to learn a time-dependent cost function from data, without imposing a specific functional form. This approach consistently outperforms traditional gravity models in accuracy while providing natural uncertainty quantification. Applying our framework to global food and agricultural trade, we show that the global South suffered disproportionately from the war in Ukraine's impact on wheat markets. We also analyze the effects of free-trade agreements and trade disputes with China, as well as Brexit's impact on British trade with Europe, uncovering hidden patterns that trade volumes alone cannot reveal.

Ensemble Inference Methods for Models With Noisy and Expensive Likelihoods

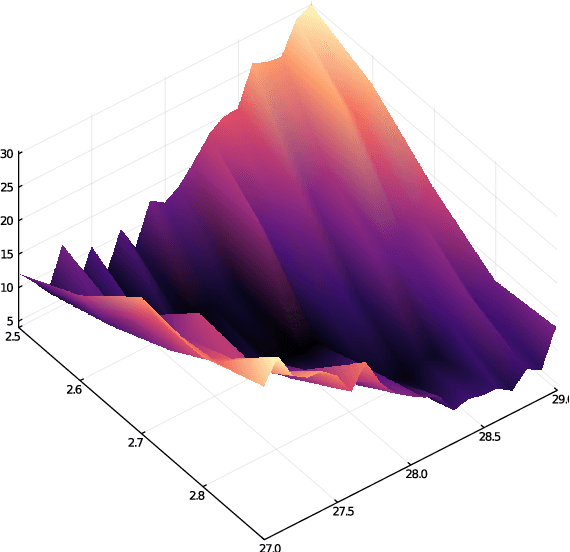
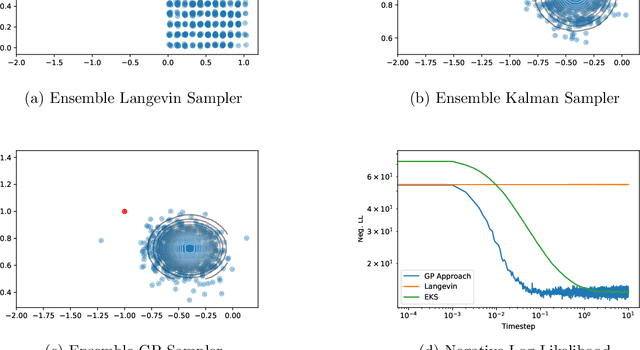
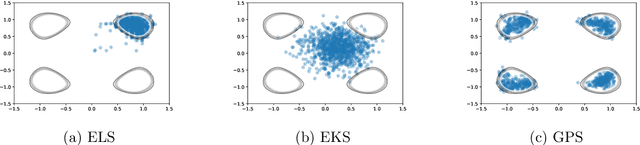
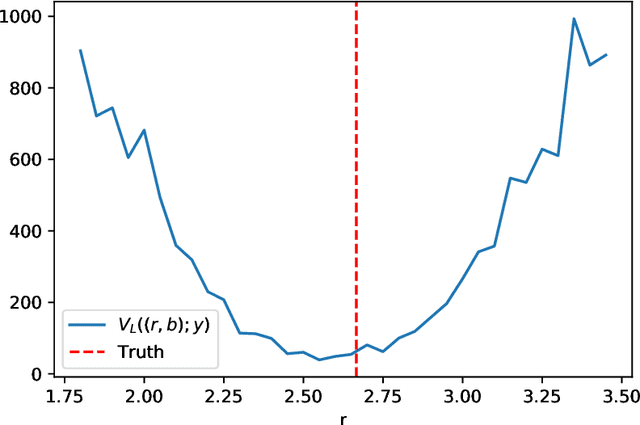
The increasing availability of data presents an opportunity to calibrate unknown parameters which appear in complex models of phenomena in the biomedical, physical and social sciences. However, model complexity often leads to parameter-to-data maps which are expensive to evaluate and are only available through noisy approximations. This paper is concerned with the use of interacting particle systems for the solution of the resulting inverse problems for parameters. Of particular interest is the case where the available forward model evaluations are subject to rapid fluctuations, in parameter space, superimposed on the smoothly varying large scale parametric structure of interest. Multiscale analysis is used to study the behaviour of interacting particle system algorithms when such rapid fluctuations, which we refer to as noise, pollute the large scale parametric dependence of the parameter-to-data map. Ensemble Kalman methods (which are derivative-free) and Langevin-based methods (which use the derivative of the parameter-to-data map) are compared in this light. The ensemble Kalman methods are shown to behave favourably in the presence of noise in the parameter-to-data map, whereas Langevin methods are adversely affected. On the other hand, Langevin methods have the correct equilibrium distribution in the setting of noise-free forward models, whilst ensemble Kalman methods only provide an uncontrolled approximation, except in the linear case. Therefore a new class of algorithms, ensemble Gaussian process samplers, which combine the benefits of both ensemble Kalman and Langevin methods, are introduced and shown to perform favourably.

On anisotropic diffusion equations for label propagation

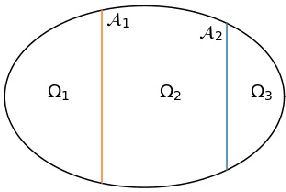
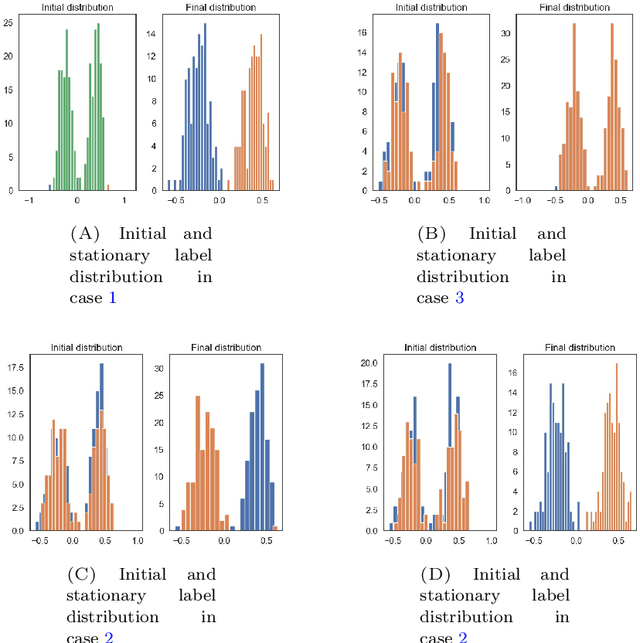
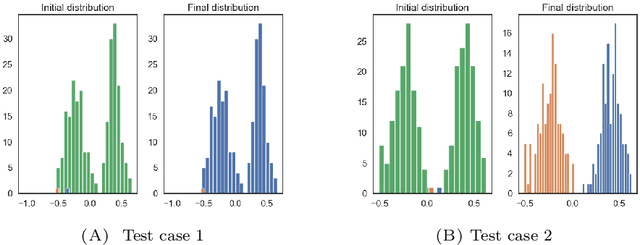
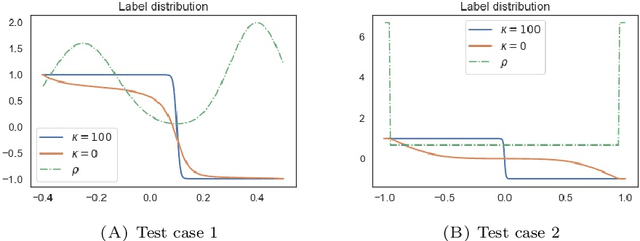
In many problems in data classification one wishes to assign labels to points in a point cloud with a certain number of them being already correctly labeled. In this paper, we propose a microscopic ODE approach, in which information about correct labels is propagated to neighboring points. Its dynamics are based on alignment mechanisms, which are often used in collective and consensus models. We derive the respective continuum description, which corresponds to an anisotropic diffusion equation with reaction term. Solutions of the continuum model inherit interesting properties of the underlying point cloud. We discuss these analytic properties and exemplify the results with micro- and macroscopic simulations.