Parallel-in-Time Solutions with Random Projection Neural Networks

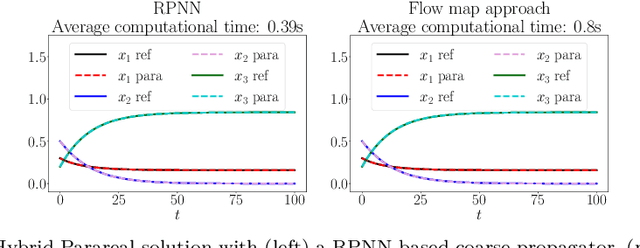
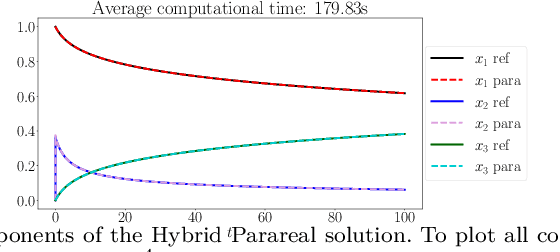
This paper considers one of the fundamental parallel-in-time methods for the solution of ordinary differential equations, Parareal, and extends it by adopting a neural network as a coarse propagator. We provide a theoretical analysis of the convergence properties of the proposed algorithm and show its effectiveness for several examples, including Lorenz and Burgers' equations. In our numerical simulations, we further specialize the underpinning neural architecture to Random Projection Neural Networks (RPNNs), a 2-layer neural network where the first layer weights are drawn at random rather than optimized. This restriction substantially increases the efficiency of fitting RPNN's weights in comparison to a standard feedforward network without negatively impacting the accuracy, as demonstrated in the SIR system example.

Learned radio interferometric imaging for varying visibility coverage

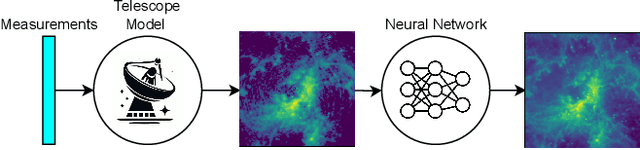
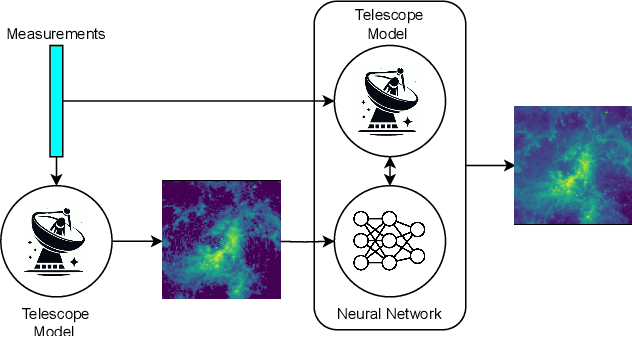
With the next generation of interferometric telescopes, such as the Square Kilometre Array (SKA), the need for highly computationally efficient reconstruction techniques is particularly acute. The challenge in designing learned, data-driven reconstruction techniques for radio interferometry is that they need to be agnostic to the varying visibility coverages of the telescope, since these are different for each observation. Because of this, learned post-processing or learned unrolled iterative reconstruction methods must typically be retrained for each specific observation, amounting to a large computational overhead. In this work we develop learned post-processing and unrolled iterative methods for varying visibility coverages, proposing training strategies to make these methods agnostic to variations in visibility coverage with minimal to no fine-tuning. Learned post-processing techniques are heavily dependent on the prior information encoded in training data and generalise poorly to other visibility coverages. In contrast, unrolled iterative methods, which include the telescope measurement operator inside the network, achieve state-of-the-art reconstruction quality and computation time, generalising well to other coverages and require little to no fine-tuning. Furthermore, they generalise well to realistic radio observations and are able to reconstruct the high dynamic range of these images.

Scalable Bayesian uncertainty quantification with data-driven priors for radio interferometric imaging

Next-generation radio interferometers like the Square Kilometer Array have the potential to unlock scientific discoveries thanks to their unprecedented angular resolution and sensitivity. One key to unlocking their potential resides in handling the deluge and complexity of incoming data. This challenge requires building radio interferometric imaging methods that can cope with the massive data sizes and provide high-quality image reconstructions with uncertainty quantification (UQ). This work proposes a method coined QuantifAI to address UQ in radio-interferometric imaging with data-driven (learned) priors for high-dimensional settings. Our model, rooted in the Bayesian framework, uses a physically motivated model for the likelihood. The model exploits a data-driven convex prior, which can encode complex information learned implicitly from simulations and guarantee the log-concavity of the posterior. We leverage probability concentration phenomena of high-dimensional log-concave posteriors that let us obtain information about the posterior, avoiding MCMC sampling techniques. We rely on convex optimisation methods to compute the MAP estimation, which is known to be faster and better scale with dimension than MCMC sampling strategies. Our method allows us to compute local credible intervals, i.e., Bayesian error bars, and perform hypothesis testing of structure on the reconstructed image. In addition, we propose a novel blazing-fast method to compute pixel-wise uncertainties at different scales. We demonstrate our method by reconstructing radio-interferometric images in a simulated setting and carrying out fast and scalable UQ, which we validate with MCMC sampling. Our method shows an improved image quality and more meaningful uncertainties than the benchmark method based on a sparsity-promoting prior. QuantifAI's source code: https://github.com/astro-informatics/QuantifAI.

Learned Interferometric Imaging for the SPIDER Instrument

The Segmented Planar Imaging Detector for Electro-Optical Reconnaissance (SPIDER) is an optical interferometric imaging device that aims to offer an alternative to the large space telescope designs of today with reduced size, weight and power consumption. This is achieved through interferometric imaging. State-of-the-art methods for reconstructing images from interferometric measurements adopt proximal optimization techniques, which are computationally expensive and require handcrafted priors. In this work we present two data-driven approaches for reconstructing images from measurements made by the SPIDER instrument. These approaches use deep learning to learn prior information from training data, increasing the reconstruction quality, and significantly reducing the computation time required to recover images by orders of magnitude. Reconstruction time is reduced to ${\sim} 10$ milliseconds, opening up the possibility of real-time imaging with SPIDER for the first time. Furthermore, we show that these methods can also be applied in domains where training data is scarce, such as astronomical imaging, by leveraging transfer learning from domains where plenty of training data are available.

On Learning the Invisible in Photoacoustic Tomography with Flat Directionally Sensitive Detector

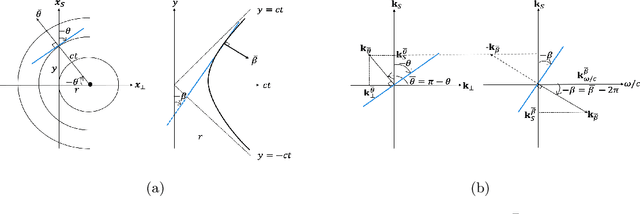
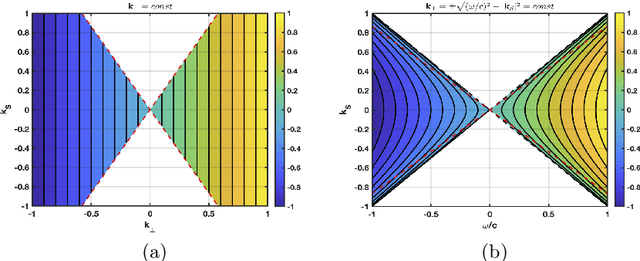
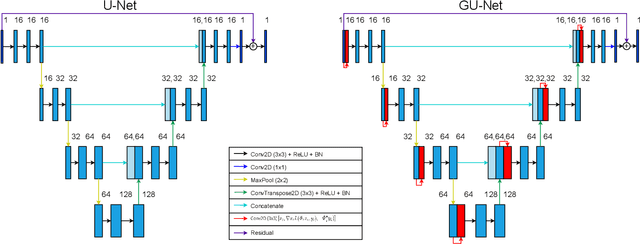
In photoacoustic tomography (PAT) with flat sensor, we routinely encounter two types of limited data. The first is due to using a finite sensor and is especially perceptible if the region of interest is large relatively to the sensor or located farther away from the sensor. In this paper, we focus on the second type caused by a varying sensitivity of the sensor to the incoming wavefront direction which can be modelled as binary i.e. by a cone of sensitivity. Such visibility conditions result, in Fourier domain, in a restriction of both the image and the data to a bowtie, akin to the one corresponding to the range of the forward operator. The visible ranges, in image and data domains, are related by the wavefront direction mapping. We adapt the wedge restricted Curvelet decomposition, we previously proposed for the representation of the full PAT data, to separate the visible and invisible wavefronts in the image. We optimally combine fast approximate operators with tailored deep neural network architectures into efficient learned reconstruction methods which perform reconstruction of the visible coefficients and the invisible coefficients are learned from a training set of similar data.

Photoacoustic Reconstruction Using Sparsity in Curvelet Frame

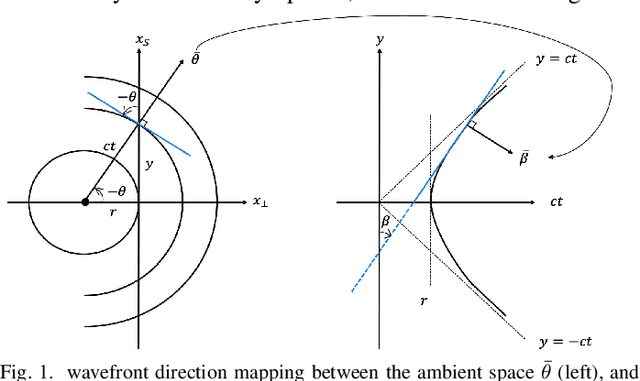
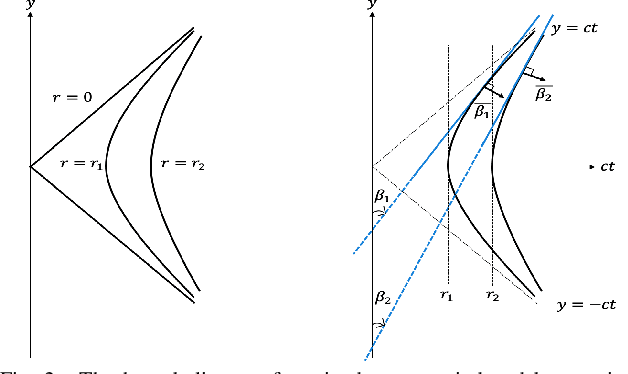
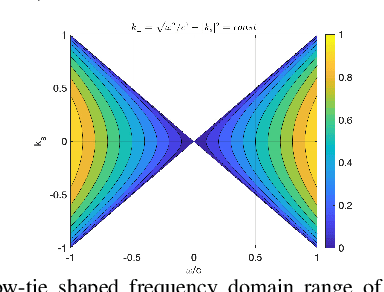
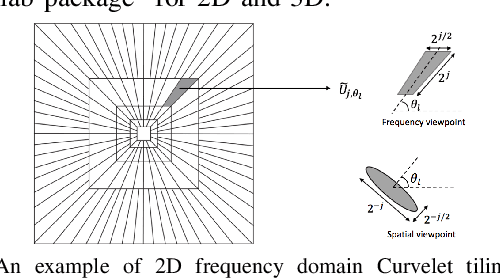
We compare two approaches to photoacoustic image reconstruction from compressed/subsampled photoacoustic data based on assumption of sparsity in the Curvelet frame: DR, a two step approach based on the recovery of the complete volume of the photoacoustic data from the subsampled data followed by the acoustic inversion, and p0R, a one step approach where the photoacoustic image (the initial pressure, p0) is directly recovered from the subsampled data. For representation of the photoacoustic data, we propose a modification of the Curvelet transform corresponding to the restriction to the range of the photoacoustic forward operator. Both recovery problems are formulated in a variational framework. As the Curvelet frame is heavily overdetermined, we use reweighted l1 norm penalties to enhance the sparsity of the solution. The data reconstruction problem DR is a standard compressed sensing recovery problem, which we solve using an ADMM-type algorithm, SALSA. Subsequently, the initial pressure is recovered using time reversal as implemented in the k-Wave Toolbox. The p0 reconstruction problem, p0R, aims to recover the photoacoustic image directly via FISTA, or ADMM when in addition including a non-negativity constraint. We compare and discuss the relative merits of the two approaches and illustrate them on 2D simulated and 3D real data.

Multi-Contrast MRI Reconstruction with Structure-Guided Total Variation

Magnetic resonance imaging (MRI) is a versatile imaging technique that allows different contrasts depending on the acquisition parameters. Many clinical imaging studies acquire MRI data for more than one of these contrasts---such as for instance T1 and T2 weighted images---which makes the overall scanning procedure very time consuming. As all of these images show the same underlying anatomy one can try to omit unnecessary measurements by taking the similarity into account during reconstruction. We will discuss two modifications of total variation---based on i) location and ii) direction---that take structural a priori knowledge into account and reduce to total variation in the degenerate case when no structural knowledge is available. We solve the resulting convex minimization problem with the alternating direction method of multipliers that separates the forward operator from the prior. For both priors the corresponding proximal operator can be implemented as an extension of the fast gradient projection method on the dual problem for total variation. We tested the priors on six data sets that are based on phantoms and real MRI images. In all test cases exploiting the structural information from the other contrast yields better results than separate reconstruction with total variation in terms of standard metrics like peak signal-to-noise ratio and structural similarity index. Furthermore, we found that exploiting the two dimensional directional information results in images with well defined edges, superior to those reconstructed solely using a priori information about the edge location.