Physics-Based Acoustic Holograms

Advances in additive manufacturing have enabled the realisation of inexpensive, scalable, diffractive acoustic lenses that can be used to generate complex acoustic fields via phase and/or amplitude modulation. However, the design of these holograms relies on a thin-element approximation adapted from optics which can severely limit the fidelity of the realised acoustic field. Here, we introduce physics-based acoustic holograms with a complex internal structure. The structures are designed using a differentiable acoustic model with manufacturing constraints via optimisation of the acoustic property distribution within the hologram. The holograms can be fabricated simply and inexpensively using contemporary 3D printers. Experimental measurements demonstrate a significant improvement compared to conventional thin-element holograms.

A Learned Born Series for Highly-Scattering Media

A new method for solving the wave equation is presented, called the learned Born series (LBS), which is derived from a convergent Born Series but its components are found through training. The LBS is shown to be significantly more accurate than the convergent Born series for the same number of iterations, in the presence of high contrast scatterers, while maintaining a comparable computational complexity. The LBS is able to generate a reasonable prediction of the global pressure field with a small number of iterations, and the errors decrease with the number of learned iterations.

j-Wave: An open-source differentiable wave simulator

We present an open-source differentiable acoustic simulator, j-Wave, which can solve time-varying and time-harmonic acoustic problems. It supports automatic differentiation, which is a program transformation technique that has many applications, especially in machine learning and scientific computing. j-Wave is composed of modular components that can be easily customized and reused. At the same time, it is compatible with some of the most popular machine learning libraries, such as JAX and TensorFlow. The accuracy of the simulation results for known configurations is evaluated against the widely used k-Wave toolbox and a cohort of acoustic simulation software. j-Wave is available from https://github.com/ucl-bug/jwave.

A research framework for writing differentiable PDE discretizations in JAX

Differentiable simulators are an emerging concept with applications in several fields, from reinforcement learning to optimal control. Their distinguishing feature is the ability to calculate analytic gradients with respect to the input parameters. Like neural networks, which are constructed by composing several building blocks called layers, a simulation often requires computing the output of an operator that can itself be decomposed into elementary units chained together. While each layer of a neural network represents a specific discrete operation, the same operator can have multiple representations, depending on the discretization employed and the research question that needs to be addressed. Here, we propose a simple design pattern to construct a library of differentiable operators and discretizations, by representing operators as mappings between families of continuous functions, parametrized by finite vectors. We demonstrate the approach on an acoustic optimization problem, where the Helmholtz equation is discretized using Fourier spectral methods, and differentiability is demonstrated using gradient descent to optimize the speed of sound of an acoustic lens. The proposed framework is open-sourced and available at \url{https://github.com/ucl-bug/jaxdf}

Photoacoustic Reconstruction Using Sparsity in Curvelet Frame

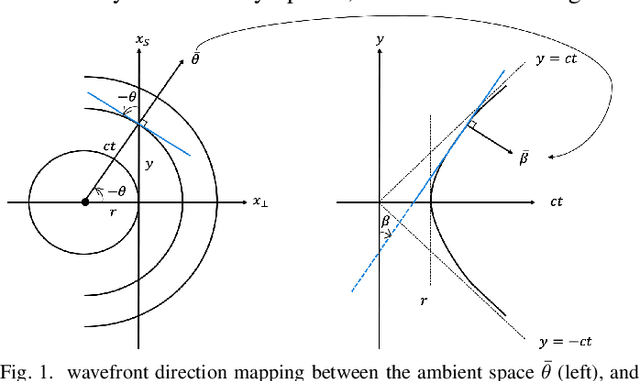
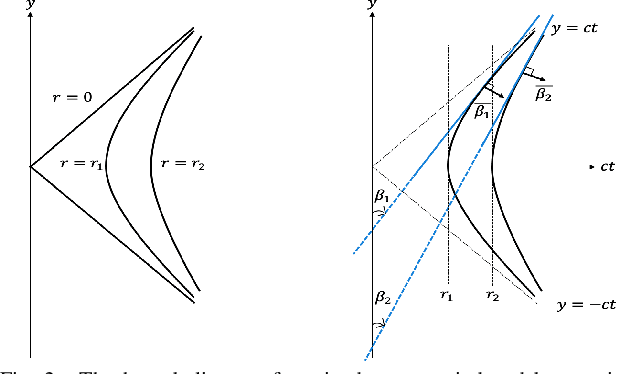
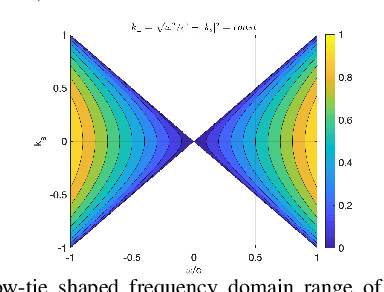
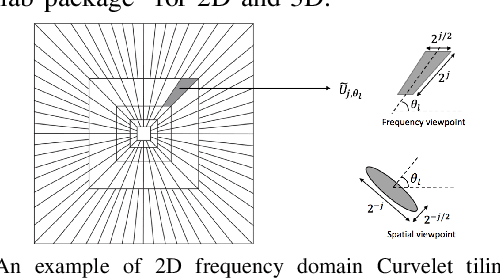
We compare two approaches to photoacoustic image reconstruction from compressed/subsampled photoacoustic data based on assumption of sparsity in the Curvelet frame: DR, a two step approach based on the recovery of the complete volume of the photoacoustic data from the subsampled data followed by the acoustic inversion, and p0R, a one step approach where the photoacoustic image (the initial pressure, p0) is directly recovered from the subsampled data. For representation of the photoacoustic data, we propose a modification of the Curvelet transform corresponding to the restriction to the range of the photoacoustic forward operator. Both recovery problems are formulated in a variational framework. As the Curvelet frame is heavily overdetermined, we use reweighted l1 norm penalties to enhance the sparsity of the solution. The data reconstruction problem DR is a standard compressed sensing recovery problem, which we solve using an ADMM-type algorithm, SALSA. Subsequently, the initial pressure is recovered using time reversal as implemented in the k-Wave Toolbox. The p0 reconstruction problem, p0R, aims to recover the photoacoustic image directly via FISTA, or ADMM when in addition including a non-negativity constraint. We compare and discuss the relative merits of the two approaches and illustrate them on 2D simulated and 3D real data.

A Helmholtz equation solver using unsupervised learning: Application to transcranial ultrasound

Transcranial ultrasound therapy is increasingly used for the non-invasive treatment of brain disorders. However, conventional numerical wave solvers are currently too computationally expensive to be used online during treatments to predict the acoustic field passing through the skull (e.g., to account for subject-specific dose and targeting variations). As a step towards real-time predictions, in the current work, a fast iterative solver for the heterogeneous Helmholtz equation in 2D is developed using a fully-learned optimizer. The lightweight network architecture is based on a modified UNet that includes a learned hidden state. The network is trained using a physics-based loss function and a set of idealized sound speed distributions with fully unsupervised training (no knowledge of the true solution is required). The learned optimizer shows excellent performance on the test set, and is capable of generalization well outside the training examples, including to much larger computational domains, and more complex source and sound speed distributions, for example, those derived from x-ray computed tomography images of the skull.