On Learning the Invisible in Photoacoustic Tomography with Flat Directionally Sensitive Detector

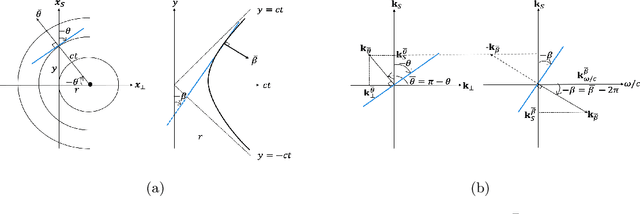
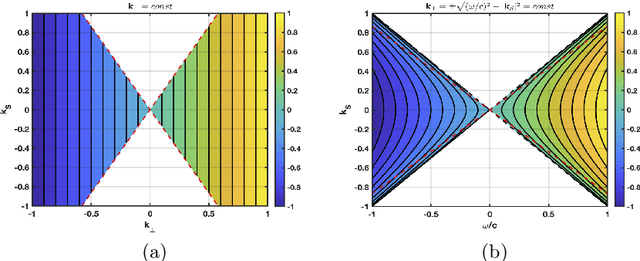
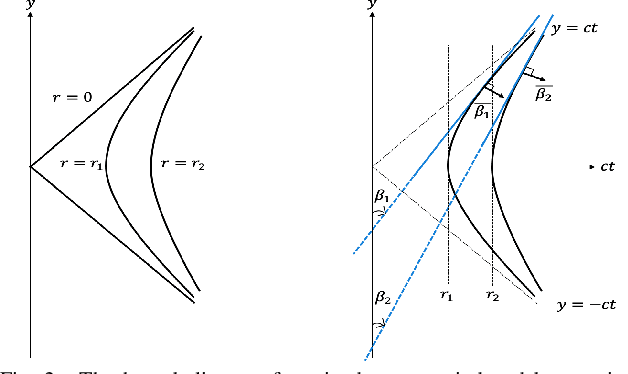
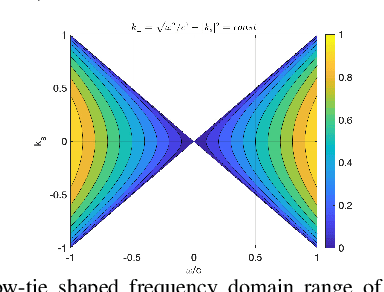
In photoacoustic tomography (PAT) with flat sensor, we routinely encounter two types of limited data. The first is due to using a finite sensor and is especially perceptible if the region of interest is large relatively to the sensor or located farther away from the sensor. In this paper, we focus on the second type caused by a varying sensitivity of the sensor to the incoming wavefront direction which can be modelled as binary i.e. by a cone of sensitivity. Such visibility conditions result, in Fourier domain, in a restriction of both the image and the data to a bowtie, akin to the one corresponding to the range of the forward operator. The visible ranges, in image and data domains, are related by the wavefront direction mapping. We adapt the wedge restricted Curvelet decomposition, we previously proposed for the representation of the full PAT data, to separate the visible and invisible wavefronts in the image. We optimally combine fast approximate operators with tailored deep neural network architectures into efficient learned reconstruction methods which perform reconstruction of the visible coefficients and the invisible coefficients are learned from a training set of similar data.

Photoacoustic Reconstruction Using Sparsity in Curvelet Frame

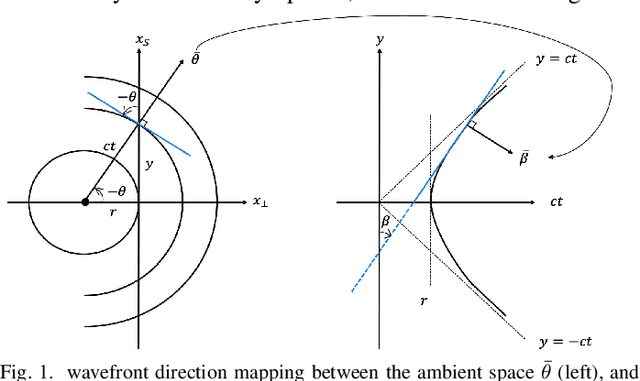
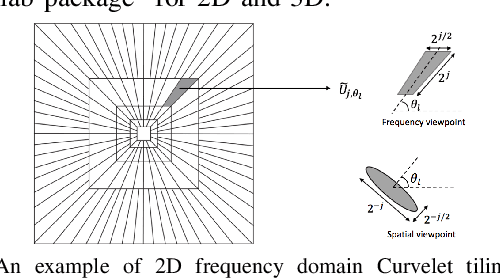
We compare two approaches to photoacoustic image reconstruction from compressed/subsampled photoacoustic data based on assumption of sparsity in the Curvelet frame: DR, a two step approach based on the recovery of the complete volume of the photoacoustic data from the subsampled data followed by the acoustic inversion, and p0R, a one step approach where the photoacoustic image (the initial pressure, p0) is directly recovered from the subsampled data. For representation of the photoacoustic data, we propose a modification of the Curvelet transform corresponding to the restriction to the range of the photoacoustic forward operator. Both recovery problems are formulated in a variational framework. As the Curvelet frame is heavily overdetermined, we use reweighted l1 norm penalties to enhance the sparsity of the solution. The data reconstruction problem DR is a standard compressed sensing recovery problem, which we solve using an ADMM-type algorithm, SALSA. Subsequently, the initial pressure is recovered using time reversal as implemented in the k-Wave Toolbox. The p0 reconstruction problem, p0R, aims to recover the photoacoustic image directly via FISTA, or ADMM when in addition including a non-negativity constraint. We compare and discuss the relative merits of the two approaches and illustrate them on 2D simulated and 3D real data.