Learned radio interferometric imaging for varying visibility coverage

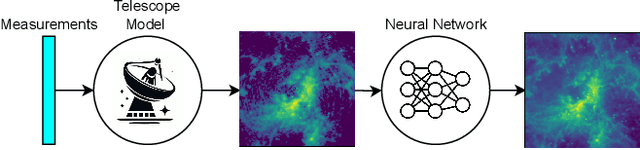
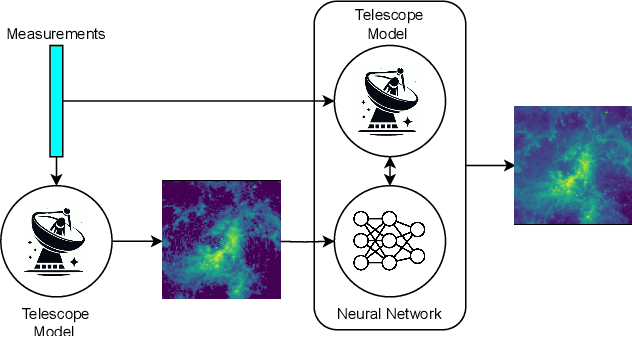
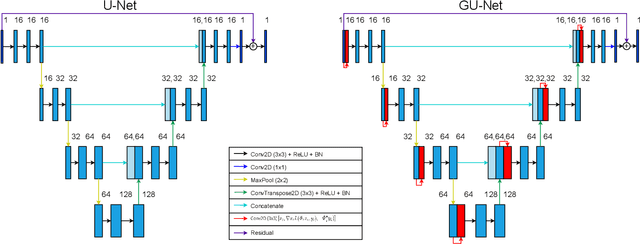
With the next generation of interferometric telescopes, such as the Square Kilometre Array (SKA), the need for highly computationally efficient reconstruction techniques is particularly acute. The challenge in designing learned, data-driven reconstruction techniques for radio interferometry is that they need to be agnostic to the varying visibility coverages of the telescope, since these are different for each observation. Because of this, learned post-processing or learned unrolled iterative reconstruction methods must typically be retrained for each specific observation, amounting to a large computational overhead. In this work we develop learned post-processing and unrolled iterative methods for varying visibility coverages, proposing training strategies to make these methods agnostic to variations in visibility coverage with minimal to no fine-tuning. Learned post-processing techniques are heavily dependent on the prior information encoded in training data and generalise poorly to other visibility coverages. In contrast, unrolled iterative methods, which include the telescope measurement operator inside the network, achieve state-of-the-art reconstruction quality and computation time, generalising well to other coverages and require little to no fine-tuning. Furthermore, they generalise well to realistic radio observations and are able to reconstruct the high dynamic range of these images.

Scalable Bayesian uncertainty quantification with data-driven priors for radio interferometric imaging

Next-generation radio interferometers like the Square Kilometer Array have the potential to unlock scientific discoveries thanks to their unprecedented angular resolution and sensitivity. One key to unlocking their potential resides in handling the deluge and complexity of incoming data. This challenge requires building radio interferometric imaging methods that can cope with the massive data sizes and provide high-quality image reconstructions with uncertainty quantification (UQ). This work proposes a method coined QuantifAI to address UQ in radio-interferometric imaging with data-driven (learned) priors for high-dimensional settings. Our model, rooted in the Bayesian framework, uses a physically motivated model for the likelihood. The model exploits a data-driven convex prior, which can encode complex information learned implicitly from simulations and guarantee the log-concavity of the posterior. We leverage probability concentration phenomena of high-dimensional log-concave posteriors that let us obtain information about the posterior, avoiding MCMC sampling techniques. We rely on convex optimisation methods to compute the MAP estimation, which is known to be faster and better scale with dimension than MCMC sampling strategies. Our method allows us to compute local credible intervals, i.e., Bayesian error bars, and perform hypothesis testing of structure on the reconstructed image. In addition, we propose a novel blazing-fast method to compute pixel-wise uncertainties at different scales. We demonstrate our method by reconstructing radio-interferometric images in a simulated setting and carrying out fast and scalable UQ, which we validate with MCMC sampling. Our method shows an improved image quality and more meaningful uncertainties than the benchmark method based on a sparsity-promoting prior. QuantifAI's source code: https://github.com/astro-informatics/QuantifAI.

Learned Interferometric Imaging for the SPIDER Instrument

The Segmented Planar Imaging Detector for Electro-Optical Reconnaissance (SPIDER) is an optical interferometric imaging device that aims to offer an alternative to the large space telescope designs of today with reduced size, weight and power consumption. This is achieved through interferometric imaging. State-of-the-art methods for reconstructing images from interferometric measurements adopt proximal optimization techniques, which are computationally expensive and require handcrafted priors. In this work we present two data-driven approaches for reconstructing images from measurements made by the SPIDER instrument. These approaches use deep learning to learn prior information from training data, increasing the reconstruction quality, and significantly reducing the computation time required to recover images by orders of magnitude. Reconstruction time is reduced to ${\sim} 10$ milliseconds, opening up the possibility of real-time imaging with SPIDER for the first time. Furthermore, we show that these methods can also be applied in domains where training data is scarce, such as astronomical imaging, by leveraging transfer learning from domains where plenty of training data are available.