Luca Pegolotti
Inferring Optical Tissue Properties from Photoplethysmography using Hybrid Amortized Inference
Oct 02, 2025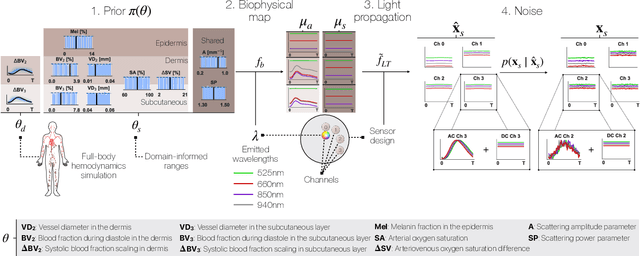
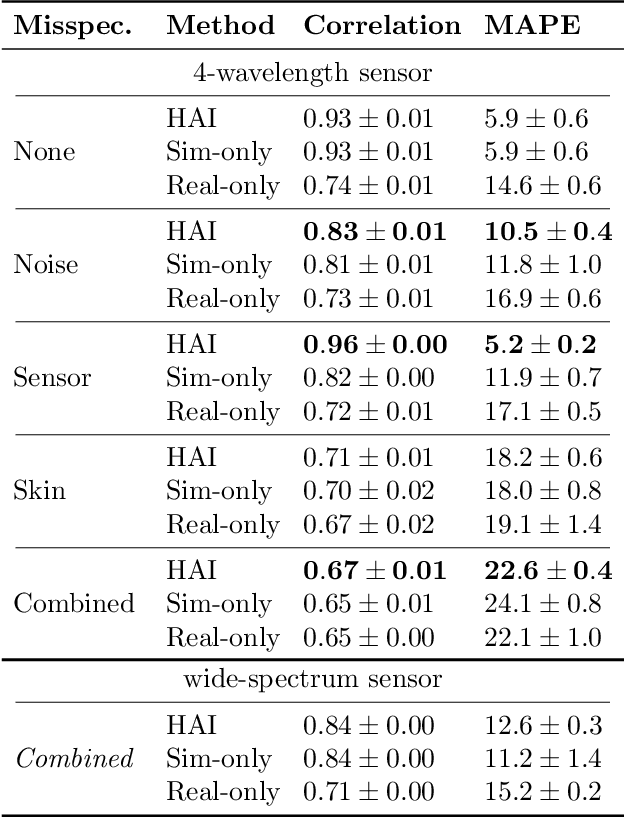
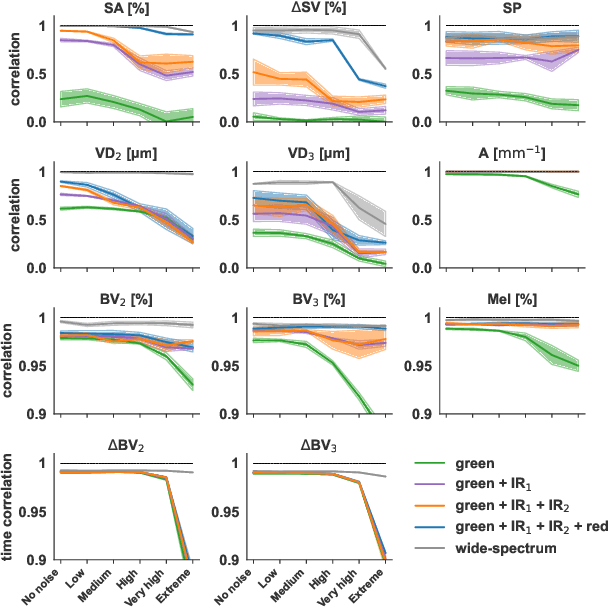

Abstract:Smart wearables enable continuous tracking of established biomarkers such as heart rate, heart rate variability, and blood oxygen saturation via photoplethysmography (PPG). Beyond these metrics, PPG waveforms contain richer physiological information, as recent deep learning (DL) studies demonstrate. However, DL models often rely on features with unclear physiological meaning, creating a tension between predictive power, clinical interpretability, and sensor design. We address this gap by introducing PPGen, a biophysical model that relates PPG signals to interpretable physiological and optical parameters. Building on PPGen, we propose hybrid amortized inference (HAI), enabling fast, robust, and scalable estimation of relevant physiological parameters from PPG signals while correcting for model misspecification. In extensive in-silico experiments, we show that HAI can accurately infer physiological parameters under diverse noise and sensor conditions. Our results illustrate a path toward PPG models that retain the fidelity needed for DL-based features while supporting clinical interpretation and informed hardware design.
Leveraging Cardiovascular Simulations for In-Vivo Prediction of Cardiac Biomarkers
Dec 23, 2024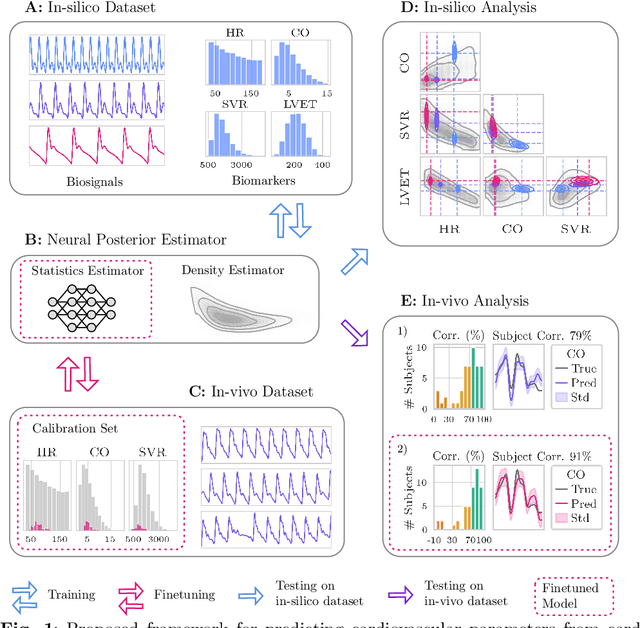
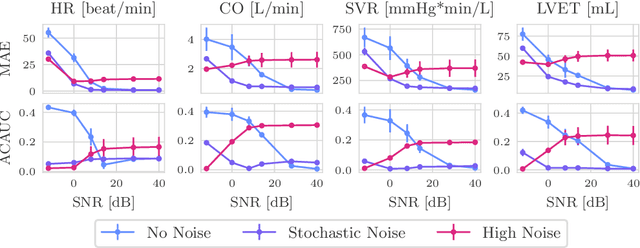
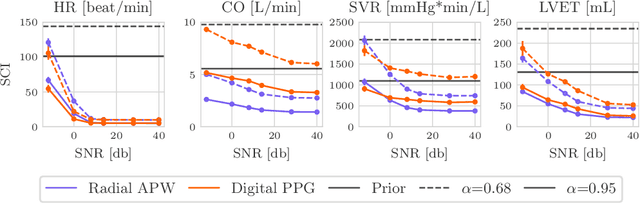
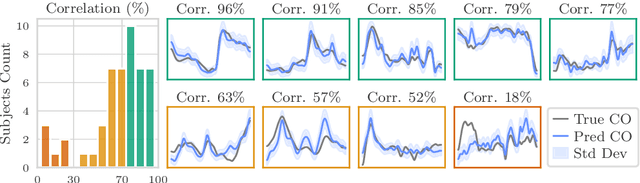
Abstract:Whole-body hemodynamics simulators, which model blood flow and pressure waveforms as functions of physiological parameters, are now essential tools for studying cardiovascular systems. However, solving the corresponding inverse problem of mapping observations (e.g., arterial pressure waveforms at specific locations in the arterial network) back to plausible physiological parameters remains challenging. Leveraging recent advances in simulation-based inference, we cast this problem as statistical inference by training an amortized neural posterior estimator on a newly built large dataset of cardiac simulations that we publicly release. To better align simulated data with real-world measurements, we incorporate stochastic elements modeling exogenous effects. The proposed framework can further integrate in-vivo data sources to refine its predictive capabilities on real-world data. In silico, we demonstrate that the proposed framework enables finely quantifying uncertainty associated with individual measurements, allowing trustworthy prediction of four biomarkers of clinical interest--namely Heart Rate, Cardiac Output, Systemic Vascular Resistance, and Left Ventricular Ejection Time--from arterial pressure waveforms and photoplethysmograms. Furthermore, we validate the framework in vivo, where our method accurately captures temporal trends in CO and SVR monitoring on the VitalDB dataset. Finally, the predictive error made by the model monotonically increases with the predicted uncertainty, thereby directly supporting the automatic rejection of unusable measurements.
Learning Reduced-Order Models for Cardiovascular Simulations with Graph Neural Networks
Mar 13, 2023



Abstract:Reduced-order models based on physics are a popular choice in cardiovascular modeling due to their efficiency, but they may experience reduced accuracy when working with anatomies that contain numerous junctions or pathological conditions. We develop one-dimensional reduced-order models that simulate blood flow dynamics using a graph neural network trained on three-dimensional hemodynamic simulation data. Given the initial condition of the system, the network iteratively predicts the pressure and flow rate at the vessel centerline nodes. Our numerical results demonstrate the accuracy and generalizability of our method in physiological geometries comprising a variety of anatomies and boundary conditions. Our findings demonstrate that our approach can achieve errors below 2% and 3% for pressure and flow rate, respectively, provided there is adequate training data. As a result, our method exhibits superior performance compared to physics-based one-dimensional models, while maintaining high efficiency at inference time.
Data driven approximation of parametrized PDEs by Reduced Basis and Neural Networks
Apr 02, 2019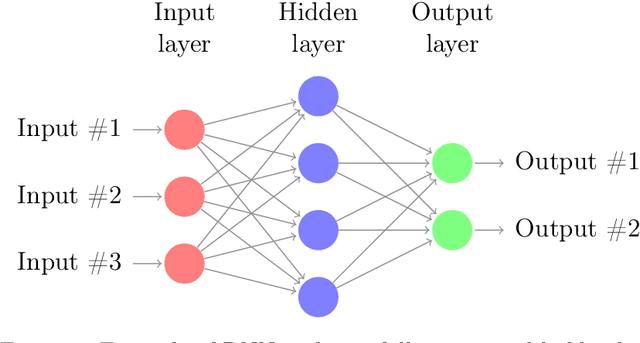
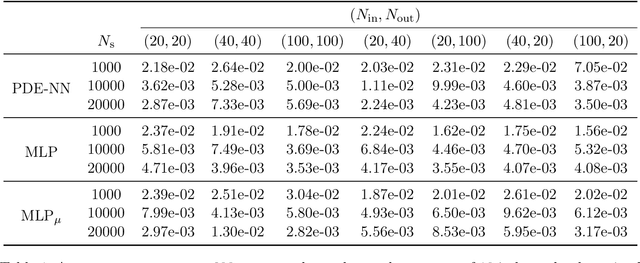
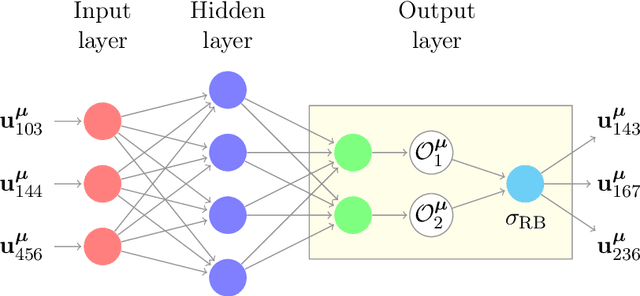

Abstract:We are interested in the approximation of partial differential equations with a data-driven approach based on the reduced basis method and machine learning. We suppose that the phenomenon of interest can be modeled by a parametrized partial differential equation, but that the value of the physical parameters is unknown or difficult to be directly measured. Our method allows to estimate fields of interest, for instance temperature of a sample of material or velocity of a fluid, given data at a handful of points in the domain. We propose to accomplish this task with a neural network embedding a reduced basis solver as exotic activation function in the last layer. The reduced basis solver accounts for the underlying physical phenomenonon and it is constructed from snapshots obtained from randomly selected values of the physical parameters during an expensive offline phase. The same full order solutions are then employed for the training of the neural network. As a matter of fact, the chosen architecture resembles an asymmetric autoencoder in which the decoder is the reduced basis solver and as such it does not contain trainable parameters. The resulting latent space of our autoencoder includes parameter-dependent quantities feeding the reduced basis solver, which -- depending on the considered partial differential equation -- are the values of the physical parameters themselves or the affine decomposition coefficients of the differential operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge