Off-Policy Maximum Entropy RL with Future State and Action Visitation Measures

We introduce a new maximum entropy reinforcement learning framework based on the distribution of states and actions visited by a policy. More precisely, an intrinsic reward function is added to the reward function of the Markov decision process that shall be controlled. For each state and action, this intrinsic reward is the relative entropy of the discounted distribution of states and actions (or features from these states and actions) visited during the next time steps. We first prove that an optimal exploration policy, which maximizes the expected discounted sum of intrinsic rewards, is also a policy that maximizes a lower bound on the state-action value function of the decision process under some assumptions. We also prove that the visitation distribution used in the intrinsic reward definition is the fixed point of a contraction operator. Following, we describe how to adapt existing algorithms to learn this fixed point and compute the intrinsic rewards to enhance exploration. A new practical off-policy maximum entropy reinforcement learning algorithm is finally introduced. Empirically, exploration policies have good state-action space coverage, and high-performing control policies are computed efficiently.

Costs Estimation in Unit Commitment Problems using Simulation-Based Inference

The Unit Commitment (UC) problem is a key optimization task in power systems to forecast the generation schedules of power units over a finite time period by minimizing costs while meeting demand and technical constraints. However, many parameters required by the UC problem are unknown, such as the costs. In this work, we estimate these unknown costs using simulation-based inference on an illustrative UC problem, which provides an approximated posterior distribution of the parameters given observed generation schedules and demands. Our results highlight that the learned posterior distribution effectively captures the underlying distribution of the data, providing a range of possible values for the unknown parameters given a past observation. This posterior allows for the estimation of past costs using observed past generation schedules, enabling operators to better forecast future costs and make more robust generation scheduling forecasts. We present avenues for future research to address overconfidence in posterior estimation, enhance the scalability of the methodology and apply it to more complex UC problems modeling the network constraints and renewable energy sources.

Reinforcement Learning for Efficient Design and Control Co-optimisation of Energy Systems

The ongoing energy transition drives the development of decentralised renewable energy sources, which are heterogeneous and weather-dependent, complicating their integration into energy systems. This study tackles this issue by introducing a novel reinforcement learning (RL) framework tailored for the co-optimisation of design and control in energy systems. Traditionally, the integration of renewable sources in the energy sector has relied on complex mathematical modelling and sequential processes. By leveraging RL's model-free capabilities, the framework eliminates the need for explicit system modelling. By optimising both control and design policies jointly, the framework enhances the integration of renewable sources and improves system efficiency. This contribution paves the way for advanced RL applications in energy management, leading to more efficient and effective use of renewable energy sources.

Behind the Myth of Exploration in Policy Gradients

Policy-gradient algorithms are effective reinforcement learning methods for solving control problems with continuous state and action spaces. To compute near-optimal policies, it is essential in practice to include exploration terms in the learning objective. Although the effectiveness of these terms is usually justified by an intrinsic need to explore environments, we propose a novel analysis and distinguish two different implications of these techniques. First, they make it possible to smooth the learning objective and to eliminate local optima while preserving the global maximum. Second, they modify the gradient estimates, increasing the probability that the stochastic parameter update eventually provides an optimal policy. In light of these effects, we discuss and illustrate empirically exploration strategies based on entropy bonuses, highlighting their limitations and opening avenues for future works in the design and analysis of such strategies.

Informed POMDP: Leveraging Additional Information in Model-Based RL

In this work, we generalize the problem of learning through interaction in a POMDP by accounting for eventual additional information available at training time. First, we introduce the informed POMDP, a new learning paradigm offering a clear distinction between the training information and the execution observation. Next, we propose an objective for learning a sufficient statistic from the history for the optimal control that leverages this information. We then show that this informed objective consists of learning an environment model from which we can sample latent trajectories. Finally, we show for the Dreamer algorithm that the convergence speed of the policies is sometimes greatly improved on several environments by using this informed environment model. Those results and the simplicity of the proposed adaptation advocate for a systematic consideration of eventual additional information when learning in a POMDP using model-based RL.

Policy Gradient Algorithms Implicitly Optimize by Continuation

Direct policy optimization in reinforcement learning is usually solved with policy-gradient algorithms, which optimize policy parameters via stochastic gradient ascent. This paper provides a new theoretical interpretation and justification of these algorithms. First, we formulate direct policy optimization in the optimization by continuation framework. The latter is a framework for optimizing nonconvex functions where a sequence of surrogate objective functions, called continuations, are locally optimized. Second, we show that optimizing affine Gaussian policies and performing entropy regularization can be interpreted as implicitly optimizing deterministic policies by continuation. Based on these theoretical results, we argue that exploration in policy-gradient algorithms consists in computing a continuation of the return of the policy at hand, and that the variance of policies should be history-dependent functions adapted to avoid local extrema rather than to maximize the return of the policy.

Recurrent networks, hidden states and beliefs in partially observable environments

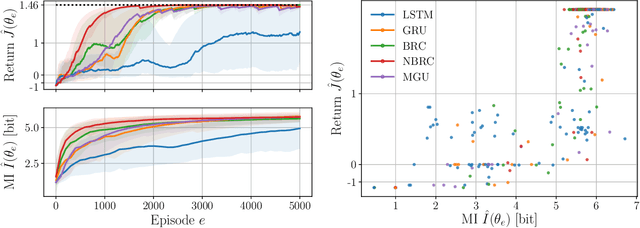
Reinforcement learning aims to learn optimal policies from interaction with environments whose dynamics are unknown. Many methods rely on the approximation of a value function to derive near-optimal policies. In partially observable environments, these functions depend on the complete sequence of observations and past actions, called the history. In this work, we show empirically that recurrent neural networks trained to approximate such value functions internally filter the posterior probability distribution of the current state given the history, called the belief. More precisely, we show that, as a recurrent neural network learns the Q-function, its hidden states become more and more correlated with the beliefs of state variables that are relevant to optimal control. This correlation is measured through their mutual information. In addition, we show that the expected return of an agent increases with the ability of its recurrent architecture to reach a high mutual information between its hidden states and the beliefs. Finally, we show that the mutual information between the hidden states and the beliefs of variables that are irrelevant for optimal control decreases through the learning process. In summary, this work shows that in its hidden states, a recurrent neural network approximating the Q-function of a partially observable environment reproduces a sufficient statistic from the history that is correlated to the relevant part of the belief for taking optimal actions.

Distributional Reinforcement Learning with Unconstrained Monotonic Neural Networks

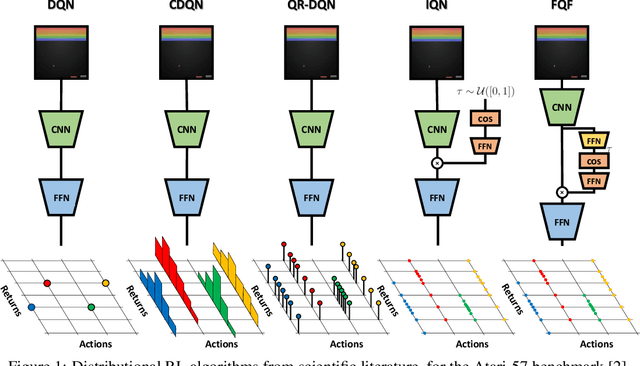
The distributional reinforcement learning (RL) approach advocates for representing the complete probability distribution of the random return instead of only modelling its expectation. A distributional RL algorithm may be characterised by two main components, namely the representation and parameterisation of the distribution and the probability metric defining the loss. This research considers the unconstrained monotonic neural network (UMNN) architecture, a universal approximator of continuous monotonic functions which is particularly well suited for modelling different representations of a distribution (PDF, CDF, quantile function). This property enables the decoupling of the effect of the function approximator class from that of the probability metric. The paper firstly introduces a methodology for learning different representations of the random return distribution. Secondly, a novel distributional RL algorithm named unconstrained monotonic deep Q-network (UMDQN) is presented. Lastly, in light of this new algorithm, an empirical comparison is performed between three probability quasimetrics, namely the Kullback-Leibler divergence, Cramer distance and Wasserstein distance. The results call for a reconsideration of all probability metrics in distributional RL, which contrasts with the dominance of the Wasserstein distance in recent publications.

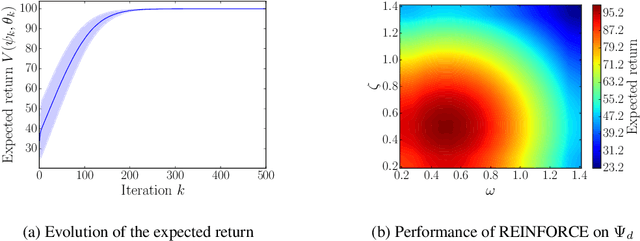
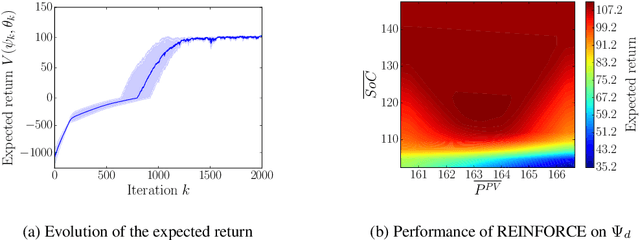
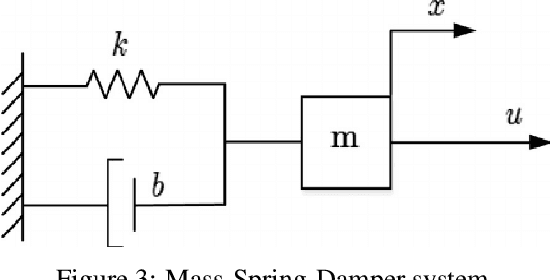
Learning optimal environments using projected stochastic gradient ascent

In this work, we generalize the direct policy search algorithms to an algorithm we call Direct Environment Search with (projected stochastic) Gradient Ascent (DESGA). The latter can be used to jointly learn a reinforcement learning (RL) environment and a policy with maximal expected return over a joint hypothesis space of environments and policies. We illustrate the performance of DESGA on two benchmarks. First, we consider a parametrized space of Mass-Spring-Damper (MSD) environments. Then, we use our algorithm for optimizing the size of the components and the operation of a small-scale and autonomous energy system, i.e. a solar off-grid microgrid, composed of photovoltaic panels, batteries, etc. The results highlight the excellent performances of the DESGA algorithm.

A Deep Reinforcement Learning Framework for Continuous Intraday Market Bidding

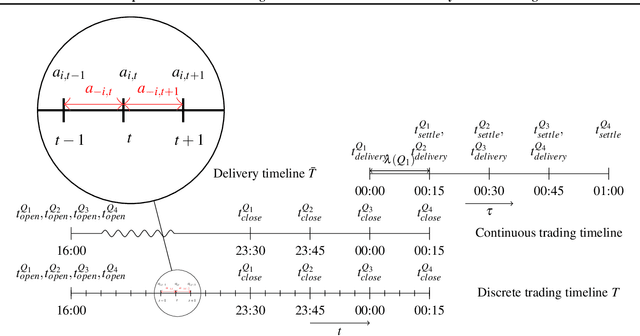
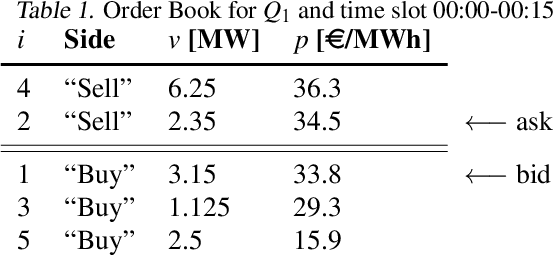
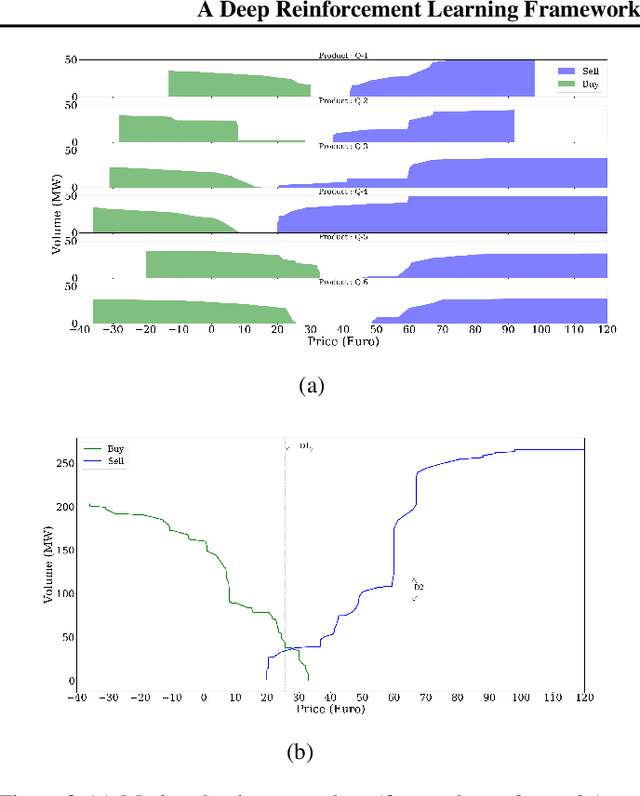
The large integration of variable energy resources is expected to shift a large part of the energy exchanges closer to real-time, where more accurate forecasts are available. In this context, the short-term electricity markets and in particular the intraday market are considered a suitable trading floor for these exchanges to occur. A key component for the successful renewable energy sources integration is the usage of energy storage. In this paper, we propose a novel modelling framework for the strategic participation of energy storage in the European continuous intraday market where exchanges occur through a centralized order book. The goal of the storage device operator is the maximization of the profits received over the entire trading horizon, while taking into account the operational constraints of the unit. The sequential decision-making problem of trading in the intraday market is modelled as a Markov Decision Process. An asynchronous distributed version of the fitted Q iteration algorithm is chosen for solving this problem due to its sample efficiency. The large and variable number of the existing orders in the order book motivates the use of high-level actions and an alternative state representation. Historical data are used for the generation of a large number of artificial trajectories in order to address exploration issues during the learning process. The resulting policy is back-tested and compared against a benchmark strategy that is the current industrial standard. Results indicate that the agent converges to a policy that achieves in average higher total revenues than the benchmark strategy.