Recurrent networks, hidden states and beliefs in partially observable environments
Paper and Code
Aug 06, 2022

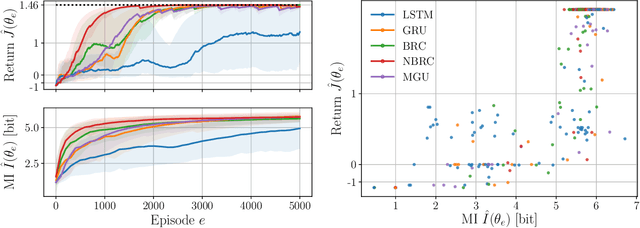

Reinforcement learning aims to learn optimal policies from interaction with environments whose dynamics are unknown. Many methods rely on the approximation of a value function to derive near-optimal policies. In partially observable environments, these functions depend on the complete sequence of observations and past actions, called the history. In this work, we show empirically that recurrent neural networks trained to approximate such value functions internally filter the posterior probability distribution of the current state given the history, called the belief. More precisely, we show that, as a recurrent neural network learns the Q-function, its hidden states become more and more correlated with the beliefs of state variables that are relevant to optimal control. This correlation is measured through their mutual information. In addition, we show that the expected return of an agent increases with the ability of its recurrent architecture to reach a high mutual information between its hidden states and the beliefs. Finally, we show that the mutual information between the hidden states and the beliefs of variables that are irrelevant for optimal control decreases through the learning process. In summary, this work shows that in its hidden states, a recurrent neural network approximating the Q-function of a partially observable environment reproduces a sufficient statistic from the history that is correlated to the relevant part of the belief for taking optimal actions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge