Distributional Reinforcement Learning with Unconstrained Monotonic Neural Networks
Paper and Code
Jun 06, 2021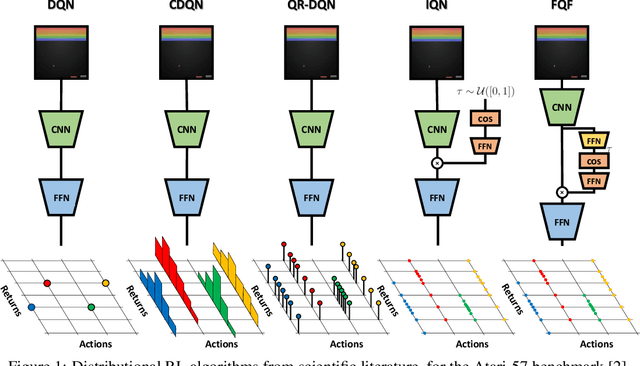



The distributional reinforcement learning (RL) approach advocates for representing the complete probability distribution of the random return instead of only modelling its expectation. A distributional RL algorithm may be characterised by two main components, namely the representation and parameterisation of the distribution and the probability metric defining the loss. This research considers the unconstrained monotonic neural network (UMNN) architecture, a universal approximator of continuous monotonic functions which is particularly well suited for modelling different representations of a distribution (PDF, CDF, quantile function). This property enables the decoupling of the effect of the function approximator class from that of the probability metric. The paper firstly introduces a methodology for learning different representations of the random return distribution. Secondly, a novel distributional RL algorithm named unconstrained monotonic deep Q-network (UMDQN) is presented. Lastly, in light of this new algorithm, an empirical comparison is performed between three probability quasimetrics, namely the Kullback-Leibler divergence, Cramer distance and Wasserstein distance. The results call for a reconsideration of all probability metrics in distributional RL, which contrasts with the dominance of the Wasserstein distance in recent publications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge