BayesFlow 2.0: Multi-Backend Amortized Bayesian Inference in Python

Modern Bayesian inference involves a mixture of computational methods for estimating, validating, and drawing conclusions from probabilistic models as part of principled workflows. An overarching motif of many Bayesian methods is that they are relatively slow, which often becomes prohibitive when fitting complex models to large data sets. Amortized Bayesian inference (ABI) offers a path to solving the computational challenges of Bayes. ABI trains neural networks on model simulations, rewarding users with rapid inference of any model-implied quantity, such as point estimates, likelihoods, or full posterior distributions. In this work, we present the Python library BayesFlow, Version 2.0, for general-purpose ABI. Along with direct posterior, likelihood, and ratio estimation, the software includes support for multiple popular deep learning backends, a rich collection of generative networks for sampling and density estimation, complete customization and high-level interfaces, as well as new capabilities for hyperparameter optimization, design optimization, and hierarchical modeling. Using a case study on dynamical system parameter estimation, combined with comparisons to similar software, we show that our streamlined, user-friendly workflow has strong potential to support broad adoption.

Sensitivity-Aware Amortized Bayesian Inference

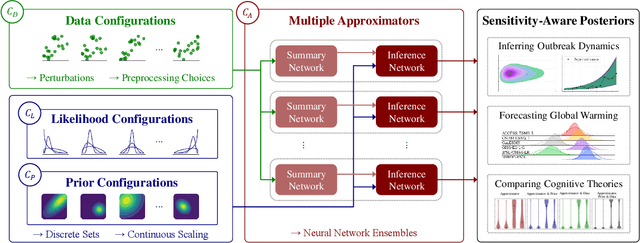
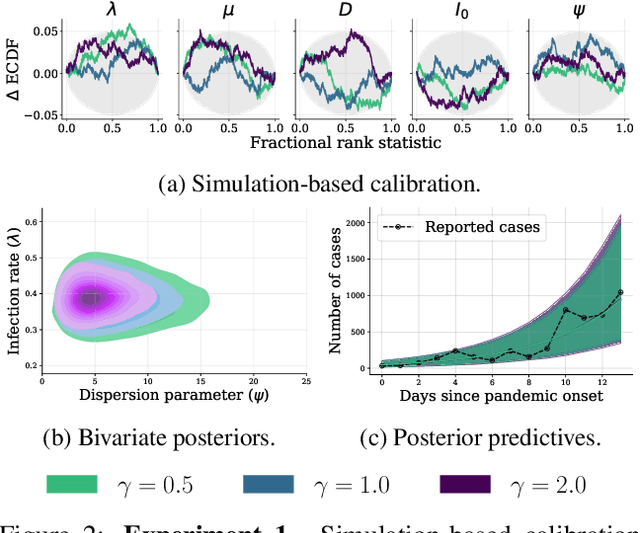
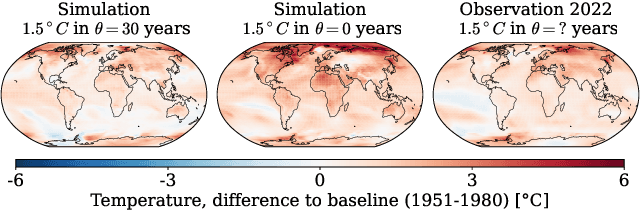
Bayesian inference is a powerful framework for making probabilistic inferences and decisions under uncertainty. Fundamental choices in modern Bayesian workflows concern the specification of the likelihood function and prior distributions, the posterior approximator, and the data. Each choice can significantly influence model-based inference and subsequent decisions, thereby necessitating sensitivity analysis. In this work, we propose a multifaceted approach to integrate sensitivity analyses into amortized Bayesian inference (ABI, i.e., simulation-based inference with neural networks). First, we utilize weight sharing to encode the structural similarities between alternative likelihood and prior specifications in the training process with minimal computational overhead. Second, we leverage the rapid inference of neural networks to assess sensitivity to various data perturbations or pre-processing procedures. In contrast to most other Bayesian approaches, both steps circumvent the costly bottleneck of refitting the model(s) for each choice of likelihood, prior, or dataset. Finally, we propose to use neural network ensembles to evaluate variation in results induced by unreliable approximation on unseen data. We demonstrate the effectiveness of our method in applied modeling problems, ranging from the estimation of disease outbreak dynamics and global warming thresholds to the comparison of human decision-making models. Our experiments showcase how our approach enables practitioners to effectively unveil hidden relationships between modeling choices and inferential conclusions.