Bayesian hierarchical stacking
Paper and Code
Jan 22, 2021
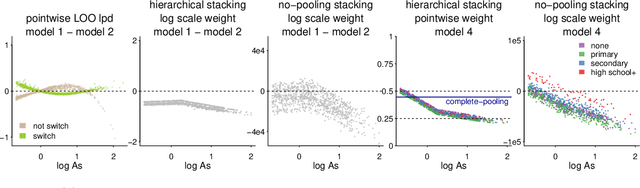
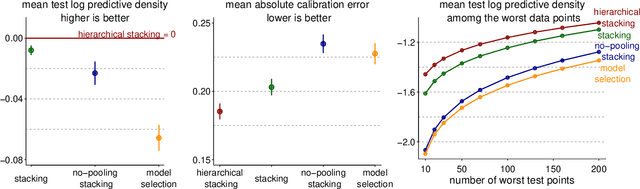
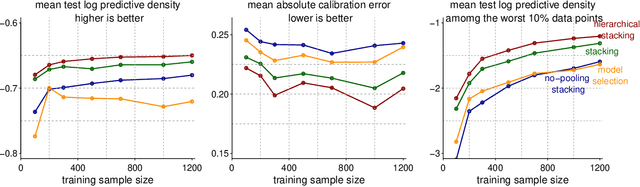
Stacking is a widely used model averaging technique that yields asymptotically optimal prediction among all linear averages. We show that stacking is most effective when the model predictive performance is heterogeneous in inputs, so that we can further improve the stacked mixture with a hierarchical model. With the input-varying yet partially-pooled model weights, hierarchical stacking improves average and conditional predictions. Our Bayesian formulation includes constant-weight (complete-pooling) stacking as a special case. We generalize to incorporate discrete and continuous inputs, other structured priors, and time-series and longitudinal data. We demonstrate on several applied problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge