Delayed rejection Hamiltonian Monte Carlo for sampling multiscale distributions

The efficiency of Hamiltonian Monte Carlo (HMC) can suffer when sampling a distribution with a wide range of length scales, because the small step sizes needed for stability in high-curvature regions are inefficient elsewhere. To address this we present a delayed rejection variant: if an initial HMC trajectory is rejected, we make one or more subsequent proposals each using a step size geometrically smaller than the last. We extend the standard delayed rejection framework by allowing the probability of a retry to depend on the probability of accepting the previous proposal. We test the scheme in several sampling tasks, including multiscale model distributions such as Neal's funnel, and statistical applications. Delayed rejection enables up to five-fold performance gains over optimally-tuned HMC, as measured by effective sample size per gradient evaluation. Even for simpler distributions, delayed rejection provides increased robustness to step size misspecification. Along the way, we provide an accessible but rigorous review of detailed balance for HMC.

Pathfinder: Parallel quasi-Newton variational inference

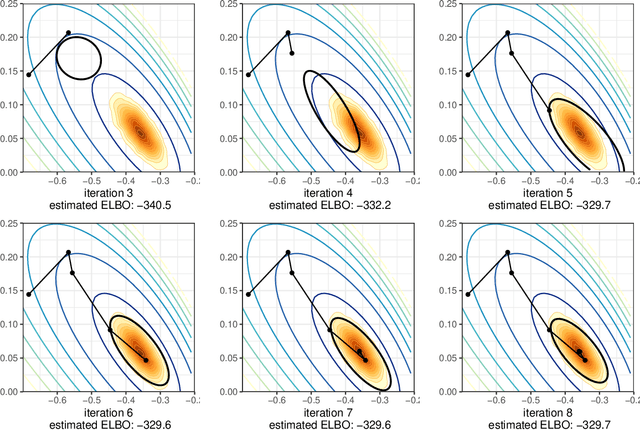
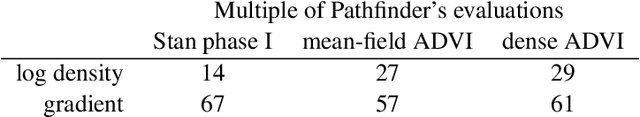
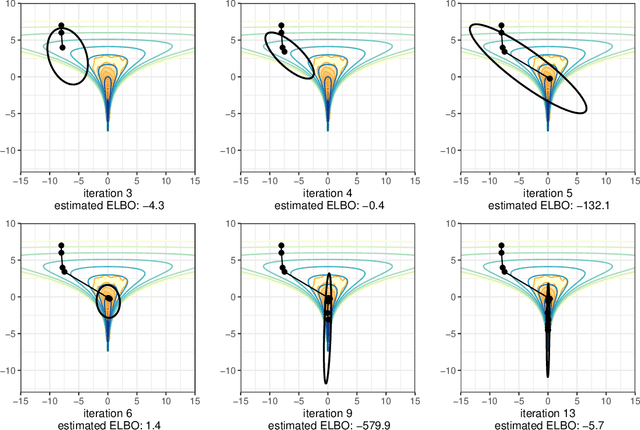
We introduce Pathfinder, a variational method for approximately sampling from differentiable log densities. Starting from a random initialization, Pathfinder locates normal approximations to the target density along a quasi-Newton optimization path, with local covariance estimated using the inverse Hessian estimates produced by the optimizer. Pathfinder returns draws from the approximation with the lowest estimated Kullback-Leibler (KL) divergence to the true posterior. We evaluate Pathfinder on a wide range of posterior distributions, demonstrating that its approximate draws are better than those from automatic differentiation variational inference (ADVI) and comparable to those produced by short chains of dynamic Hamiltonian Monte Carlo (HMC), as measured by 1-Wasserstein distance. Compared to ADVI and short dynamic HMC runs, Pathfinder requires one to two orders of magnitude fewer log density and gradient evaluations, with greater reductions for more challenging posteriors. Importance resampling over multiple runs of Pathfinder improves the diversity of approximate draws, reducing 1-Wasserstein distance further and providing a measure of robustness to optimization failures on plateaus, saddle points, or in minor modes. The Monte Carlo KL-divergence estimates are embarrassingly parallelizable in the core Pathfinder algorithm, as are multiple runs in the resampling version, further increasing Pathfinder's speed advantage with multiple cores.

Probabilistic Parsing Using Left Corner Language Models

We introduce a novel parser based on a probabilistic version of a left-corner parser. The left-corner strategy is attractive because rule probabilities can be conditioned on both top-down goals and bottom-up derivations. We develop the underlying theory and explain how a grammar can be induced from analyzed data. We show that the left-corner approach provides an advantage over simple top-down probabilistic context-free grammars in parsing the Wall Street Journal using a grammar induced from the Penn Treebank. We also conclude that the Penn Treebank provides a fairly weak testbed due to the flatness of its bracketings and to the obvious overgeneration and undergeneration of its induced grammar.