Neural Quantum States in Mixed Precision

Scientific computing has long relied on double precision (64-bit floating point) arithmetic to guarantee accuracy in simulations of real-world phenomena. However, the growing availability of hardware accelerators such as Graphics Processing Units (GPUs) has made low-precision formats attractive due to their superior performance, reduced memory footprint, and improved energy efficiency. In this work, we investigate the role of mixed-precision arithmetic in neural-network based Variational Monte Carlo (VMC), a widely used method for solving computationally otherwise intractable quantum many-body systems. We first derive general analytical bounds on the error introduced by reduced precision on Metropolis-Hastings MCMC, and then empirically validate these bounds on the use-case of VMC. We demonstrate that significant portions of the algorithm, in particular, sampling the quantum state, can be executed in half precision without loss of accuracy. More broadly, this work provides a theoretical framework to assess the applicability of mixed-precision arithmetic in machine-learning approaches that rely on MCMC sampling. In the context of VMC, we additionally demonstrate the practical effectiveness of mixed-precision strategies, enabling more scalable and energy-efficient simulations of quantum many-body systems.

Tail-Sensitive KL and Rényi Convergence of Unadjusted Hamiltonian Monte Carlo via One-Shot Couplings

Hamiltonian Monte Carlo (HMC) algorithms are among the most widely used sampling methods in high dimensional settings, yet their convergence properties are poorly understood in divergences that quantify relative density mismatch, such as Kullback-Leibler (KL) and Rényi divergences. These divergences naturally govern acceptance probabilities and warm-start requirements for Metropolis-adjusted Markov chains. In this work, we develop a framework for upgrading Wasserstein convergence guarantees for unadjusted Hamiltonian Monte Carlo (uHMC) to guarantees in tail-sensitive KL and Rényi divergences. Our approach is based on one-shot couplings, which we use to establish a regularization property of the uHMC transition kernel. This regularization allows Wasserstein-2 mixing-time and asymptotic bias bounds to be lifted to KL divergence, and analogous Orlicz-Wasserstein bounds to be lifted to Rényi divergence, paralleling earlier work of Bou-Rabee and Eberle (2023) that upgrade Wasserstein-1 bounds to total variation distance via kernel smoothing. As a consequence, our results provide quantitative control of relative density mismatch, clarify the role of discretization bias in strong divergences, and yield principled guarantees relevant both for unadjusted sampling and for generating warm starts for Metropolis-adjusted Markov chains.

Ballistic Convergence in Hit-and-Run Monte Carlo and a Coordinate-free Randomized Kaczmarz Algorithm

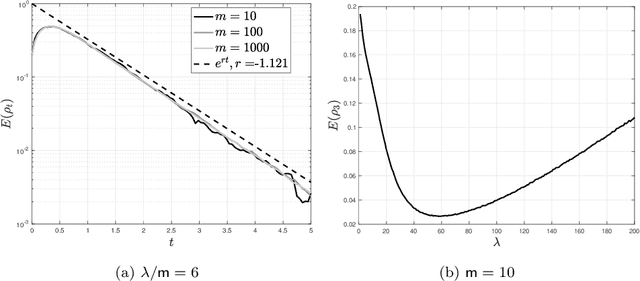
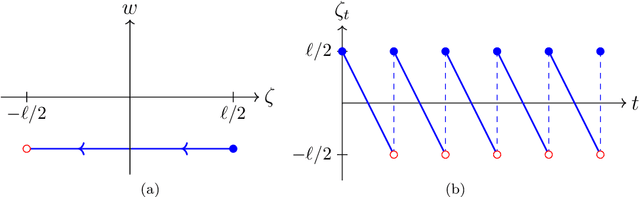
Hit-and-Run is a coordinate-free Gibbs sampler, yet the quantitative advantages of its coordinate-free property remain largely unexplored beyond empirical studies. In this paper, we prove sharp estimates for the Wasserstein contraction of Hit-and-Run in Gaussian target measures via coupling methods and conclude mixing time bounds. Our results uncover ballistic and superdiffusive convergence rates in certain settings. Furthermore, we extend these insights to a coordinate-free variant of the randomized Kaczmarz algorithm, an iterative method for linear systems, and demonstrate analogous convergence rates. These findings offer new insights into the advantages and limitations of coordinate-free methods for both sampling and optimization.

Mixing of the No-U-Turn Sampler and the Geometry of Gaussian Concentration

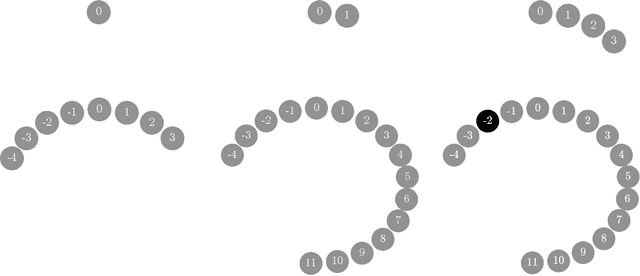
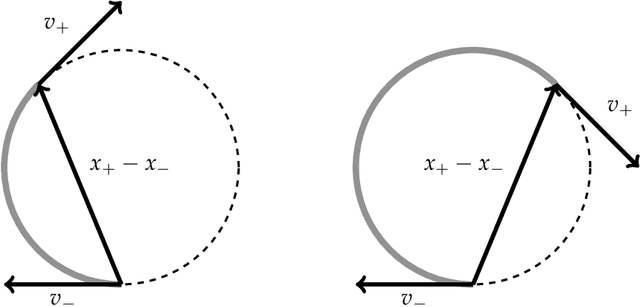
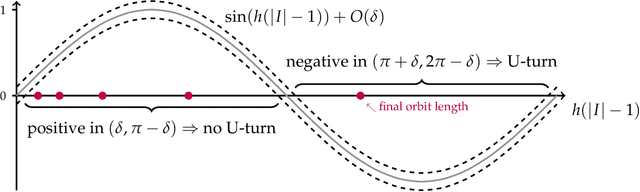
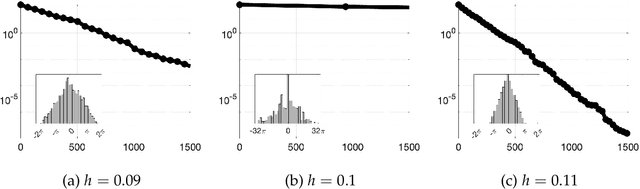
We prove that the mixing time of the No-U-Turn Sampler (NUTS), when initialized in the concentration region of the canonical Gaussian measure, scales as $d^{1/4}$, up to logarithmic factors, where $d$ is the dimension. This scaling is expected to be sharp. This result is based on a coupling argument that leverages the geometric structure of the target distribution. Specifically, concentration of measure results in a striking uniformity in NUTS' locally adapted transitions, which holds with high probability. This uniformity is formalized by interpreting NUTS as an accept/reject Markov chain, where the mixing properties for the more uniform accept chain are analytically tractable. Additionally, our analysis uncovers a previously unnoticed issue with the path length adaptation procedure of NUTS, specifically related to looping behavior, which we address in detail.

GIST: Gibbs self-tuning for locally adaptive Hamiltonian Monte Carlo

We present a novel and flexible framework for localized tuning of Hamiltonian Monte Carlo samplers by sampling the algorithm's tuning parameters conditionally based on the position and momentum at each step. For adaptively sampling path lengths, we show that randomized Hamiltonian Monte Carlo, the No-U-Turn Sampler, and the Apogee-to-Apogee Path Sampler all fit within this unified framework as special cases. The framework is illustrated with a simple alternative to the No-U-Turn Sampler for locally adapting path lengths.

Randomized Runge-Kutta-Nyström

We present 5/2- and 7/2-order $L^2$-accurate randomized Runge-Kutta-Nystr\"om methods to approximate the Hamiltonian flow underlying various non-reversible Markov chain Monte Carlo chains including unadjusted Hamiltonian Monte Carlo and unadjusted kinetic Langevin chains. Quantitative 5/2-order $L^2$-accuracy upper bounds are provided under gradient and Hessian Lipschitz assumptions on the potential energy function. The superior complexity of the corresponding Markov chains is numerically demonstrated for a selection of `well-behaved', high-dimensional target distributions.

Unadjusted Hamiltonian MCMC with Stratified Monte Carlo Time Integration

A novel randomized time integrator is suggested for unadjusted Hamiltonian Monte Carlo (uHMC) in place of the usual Verlet integrator; namely, a stratified Monte Carlo (sMC) integrator which involves a minor modification to Verlet, and hence, is easy to implement. For target distributions of the form $\mu(dx) \propto e^{-U(x)} dx$ where $U: \mathbb{R}^d \to \mathbb{R}_{\ge 0}$ is both $K$-strongly convex and $L$-gradient Lipschitz, and initial distributions $\nu$ with finite second moment, coupling proofs reveal that an $\varepsilon$-accurate approximation of the target distribution $\mu$ in $L^2$-Wasserstein distance $\boldsymbol{\mathcal{W}}^2$ can be achieved by the uHMC algorithm with sMC time integration using $O\left((d/K)^{1/3} (L/K)^{5/3} \varepsilon^{-2/3} \log( \boldsymbol{\mathcal{W}}^2(\mu, \nu) / \varepsilon)^+\right)$ gradient evaluations; whereas without additional assumptions the corresponding complexity of the uHMC algorithm with Verlet time integration is in general $O\left((d/K)^{1/2} (L/K)^2 \varepsilon^{-1} \log( \boldsymbol{\mathcal{W}}^2(\mu, \nu) / \varepsilon)^+ \right)$. Duration randomization, which has a similar effect as partial momentum refreshment, is also treated. In this case, without additional assumptions on the target distribution, the complexity of duration-randomized uHMC with sMC time integration improves to $O\left(\max\left((d/K)^{1/4} (L/K)^{3/2} \varepsilon^{-1/2},(d/K)^{1/3} (L/K)^{4/3} \varepsilon^{-2/3} \right) \right)$ up to logarithmic factors. The improvement due to duration randomization turns out to be analogous to that of time integrator randomization.

Mixing Time Guarantees for Unadjusted Hamiltonian Monte Carlo

We provide quantitative upper bounds on the total variation mixing time of the Markov chain corresponding to the unadjusted Hamiltonian Monte Carlo (uHMC) algorithm. For two general classes of models and fixed time discretization step size $h$, the mixing time is shown to depend only logarithmically on the dimension. Moreover, we provide quantitative upper bounds on the total variation distance between the invariant measure of the uHMC chain and the true target measure. As a consequence, we show that an $\varepsilon$-accurate approximation of the target distribution $\mu$ in total variation distance can be achieved by uHMC for a broad class of models with $O\left(d^{3/4}\varepsilon^{-1/2}\log (d/\varepsilon )\right)$ gradient evaluations, and for mean field models with weak interactions with $O\left(d^{1/2}\varepsilon^{-1/2}\log (d/\varepsilon )\right)$ gradient evaluations. The proofs are based on the construction of successful couplings for uHMC that realize the upper bounds.

Couplings for Andersen Dynamics

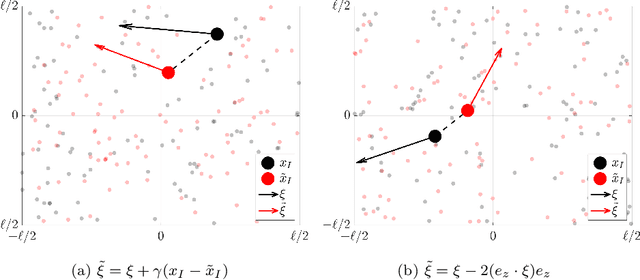
Andersen dynamics is a standard method for molecular simulations, and a precursor of the Hamiltonian Monte Carlo algorithm used in MCMC inference. The stochastic process corresponding to Andersen dynamics is a PDMP (piecewise deterministic Markov process) that iterates between Hamiltonian flows and velocity randomizations of randomly selected particles. Both from the viewpoint of molecular dynamics and MCMC inference, a basic question is to understand the convergence to equilibrium of this PDMP particularly in high dimension. Here we present couplings to obtain sharp convergence bounds in the Wasserstein sense that do not require global convexity of the underlying potential energy.

Coupling and Convergence for Hamiltonian Monte Carlo

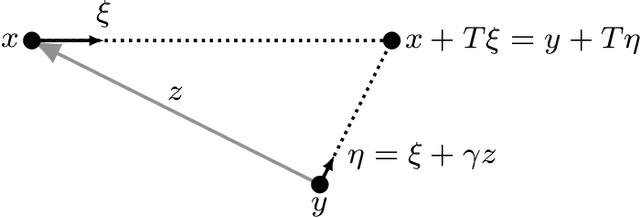
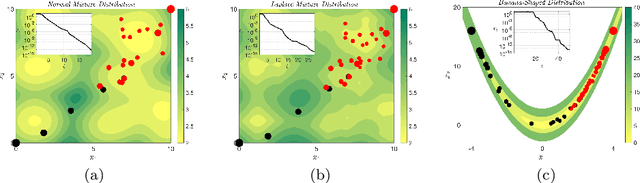
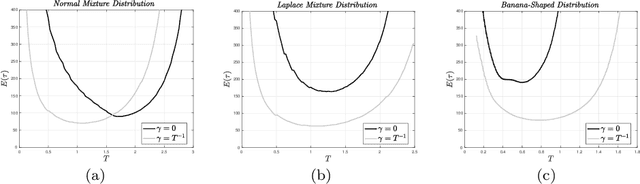
Based on a new coupling approach, we prove that the transition step of the Hamiltonian Monte Carlo algorithm is contractive w.r.t. a carefully designed Kantorovich (L1 Wasserstein) distance. The lower bound for the contraction rate is explicit. Global convexity of the potential is not required, and thus multimodal target distributions are included. Explicit quantitative bounds for the number of steps required to approximate the stationary distribution up to a given error are a direct consequence of contractivity. These bounds show that HMC can overcome diffusive behaviour if the duration of the Hamiltonian dynamics is adjusted appropriately.