Ballistic Convergence in Hit-and-Run Monte Carlo and a Coordinate-free Randomized Kaczmarz Algorithm

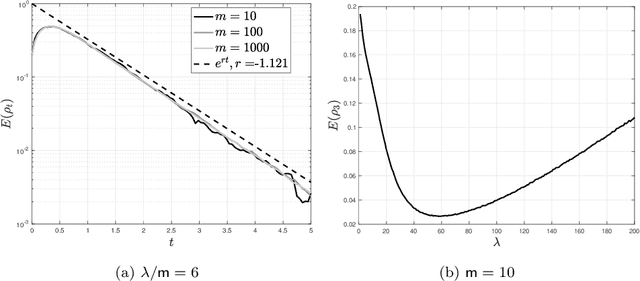
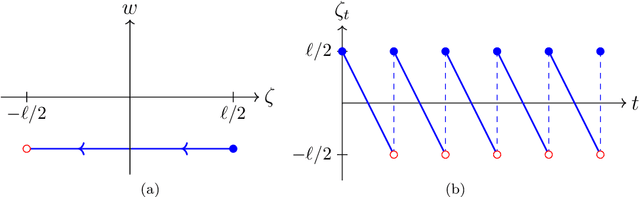
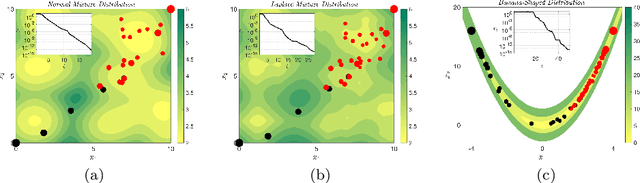
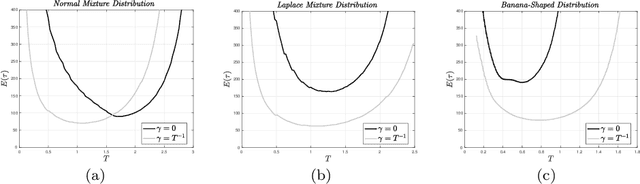
Hit-and-Run is a coordinate-free Gibbs sampler, yet the quantitative advantages of its coordinate-free property remain largely unexplored beyond empirical studies. In this paper, we prove sharp estimates for the Wasserstein contraction of Hit-and-Run in Gaussian target measures via coupling methods and conclude mixing time bounds. Our results uncover ballistic and superdiffusive convergence rates in certain settings. Furthermore, we extend these insights to a coordinate-free variant of the randomized Kaczmarz algorithm, an iterative method for linear systems, and demonstrate analogous convergence rates. These findings offer new insights into the advantages and limitations of coordinate-free methods for both sampling and optimization.

Asymptotic bias of inexact Markov Chain Monte Carlo methods in high dimension

This paper establishes non-asymptotic bounds on Wasserstein distances between the invariant probability measures of inexact MCMC methods and their target distribution. In particular, the results apply to the unadjusted Langevin algorithm and to unadjusted Hamiltonian Monte Carlo, but also to methods relying on other discretization schemes. Our focus is on understanding the precise dependence of the accuracy on both the dimension and the discretization step size. We show that the dimension dependence relies on some key quantities. As a consequence, the same dependence on the step size and the dimension as in the product case can be recovered for several important classes of models. On the other hand, for more general models, the dimension dependence of the asymptotic bias may be worse than in the product case even if the exact dynamics has dimension-free mixing properties.

Mixing Time Guarantees for Unadjusted Hamiltonian Monte Carlo

We provide quantitative upper bounds on the total variation mixing time of the Markov chain corresponding to the unadjusted Hamiltonian Monte Carlo (uHMC) algorithm. For two general classes of models and fixed time discretization step size $h$, the mixing time is shown to depend only logarithmically on the dimension. Moreover, we provide quantitative upper bounds on the total variation distance between the invariant measure of the uHMC chain and the true target measure. As a consequence, we show that an $\varepsilon$-accurate approximation of the target distribution $\mu$ in total variation distance can be achieved by uHMC for a broad class of models with $O\left(d^{3/4}\varepsilon^{-1/2}\log (d/\varepsilon )\right)$ gradient evaluations, and for mean field models with weak interactions with $O\left(d^{1/2}\varepsilon^{-1/2}\log (d/\varepsilon )\right)$ gradient evaluations. The proofs are based on the construction of successful couplings for uHMC that realize the upper bounds.

Couplings for Andersen Dynamics

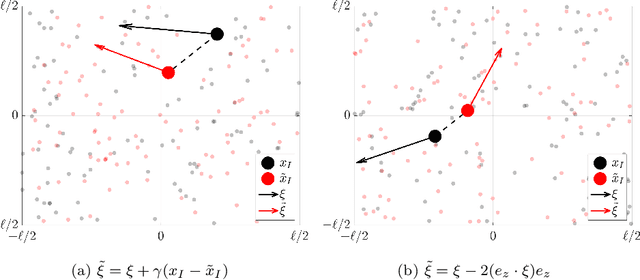
Andersen dynamics is a standard method for molecular simulations, and a precursor of the Hamiltonian Monte Carlo algorithm used in MCMC inference. The stochastic process corresponding to Andersen dynamics is a PDMP (piecewise deterministic Markov process) that iterates between Hamiltonian flows and velocity randomizations of randomly selected particles. Both from the viewpoint of molecular dynamics and MCMC inference, a basic question is to understand the convergence to equilibrium of this PDMP particularly in high dimension. Here we present couplings to obtain sharp convergence bounds in the Wasserstein sense that do not require global convexity of the underlying potential energy.

Coupling and Convergence for Hamiltonian Monte Carlo

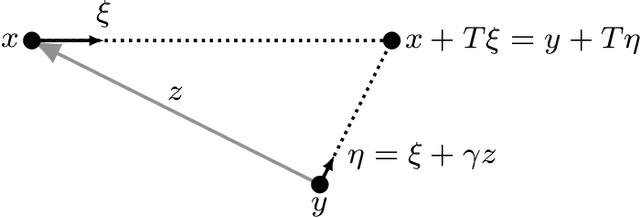
Based on a new coupling approach, we prove that the transition step of the Hamiltonian Monte Carlo algorithm is contractive w.r.t. a carefully designed Kantorovich (L1 Wasserstein) distance. The lower bound for the contraction rate is explicit. Global convexity of the potential is not required, and thus multimodal target distributions are included. Explicit quantitative bounds for the number of steps required to approximate the stationary distribution up to a given error are a direct consequence of contractivity. These bounds show that HMC can overcome diffusive behaviour if the duration of the Hamiltonian dynamics is adjusted appropriately.

A Pose-Sensitive Embedding for Person Re-Identification with Expanded Cross Neighborhood Re-Ranking

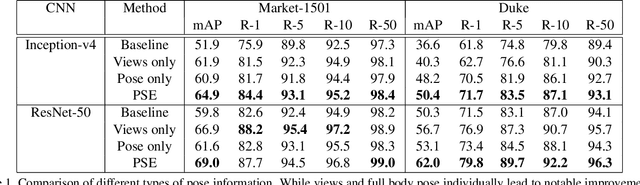
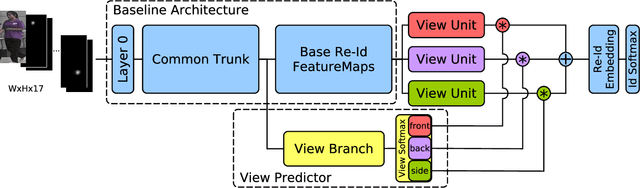
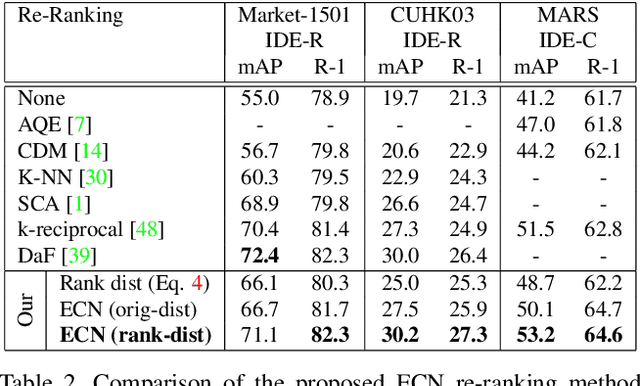
Person re identification is a challenging retrieval task that requires matching a person's acquired image across non overlapping camera views. In this paper we propose an effective approach that incorporates both the fine and coarse pose information of the person to learn a discriminative embedding. In contrast to the recent direction of explicitly modeling body parts or correcting for misalignment based on these, we show that a rather straightforward inclusion of acquired camera view and/or the detected joint locations into a convolutional neural network helps to learn a very effective representation. To increase retrieval performance, re-ranking techniques based on computed distances have recently gained much attention. We propose a new unsupervised and automatic re-ranking framework that achieves state-of-the-art re-ranking performance. We show that in contrast to the current state-of-the-art re-ranking methods our approach does not require to compute new rank lists for each image pair (e.g., based on reciprocal neighbors) and performs well by using simple direct rank list based comparison or even by just using the already computed euclidean distances between the images. We show that both our learned representation and our re-ranking method achieve state-of-the-art performance on a number of challenging surveillance image and video datasets. The code is available online at: https://github.com/pse-ecn/pose-sensitive-embedding

Pose-Driven Deep Models for Person Re-Identification

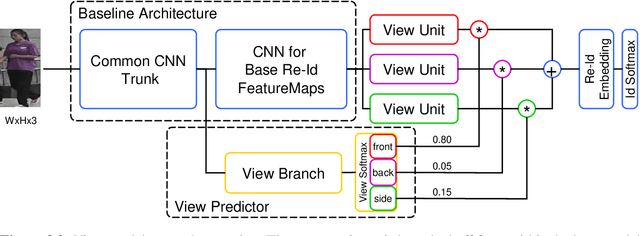
Person re-identification (re-id) is the task of recognizing and matching persons at different locations recorded by cameras with non-overlapping views. One of the main challenges of re-id is the large variance in person poses and camera angles since neither of them can be influenced by the re-id system. In this work, an effective approach to integrate coarse camera view information as well as fine-grained pose information into a convolutional neural network (CNN) model for learning discriminative re-id embeddings is introduced. In most recent work pose information is either explicitly modeled within the re-id system or explicitly used for pre-processing, for example by pose-normalizing person images. In contrast, the proposed approach shows that a direct use of camera view as well as the detected body joint locations into a standard CNN can be used to significantly improve the robustness of learned re-id embeddings. On four challenging surveillance and video re-id datasets significant improvements over the current state of the art have been achieved. Furthermore, a novel reordering of the MARS dataset, called X-MARS is introduced to allow cross-validation of models trained for single-image re-id on tracklet data.