On Accelerated Mixing of the No-U-turn Sampler

Recent progress on the theory of variational hypocoercivity established that Randomized Hamiltonian Monte Carlo -- at criticality -- can achieve pronounced acceleration in its convergence and hence sampling performance over diffusive dynamics. Manual critical tuning being unfeasible in practice has motivated automated algorithmic solutions, notably the No-U-turn Sampler. Beyond its empirical success, a rigorous study of this method's ability to achieve accelerated convergence has been missing. We initiate this investigation combining a concentration of measure approach to examine the automatic tuning mechanism with a coupling based mixing analysis for Hamiltonian Monte Carlo. In certain Gaussian target distributions, this yields a precise characterization of the sampler's behavior resulting, in particular, in rigorous mixing guarantees describing the algorithm's ability and limitations in achieving accelerated convergence.

Ballistic Convergence in Hit-and-Run Monte Carlo and a Coordinate-free Randomized Kaczmarz Algorithm

Hit-and-Run is a coordinate-free Gibbs sampler, yet the quantitative advantages of its coordinate-free property remain largely unexplored beyond empirical studies. In this paper, we prove sharp estimates for the Wasserstein contraction of Hit-and-Run in Gaussian target measures via coupling methods and conclude mixing time bounds. Our results uncover ballistic and superdiffusive convergence rates in certain settings. Furthermore, we extend these insights to a coordinate-free variant of the randomized Kaczmarz algorithm, an iterative method for linear systems, and demonstrate analogous convergence rates. These findings offer new insights into the advantages and limitations of coordinate-free methods for both sampling and optimization.

Mixing of the No-U-Turn Sampler and the Geometry of Gaussian Concentration

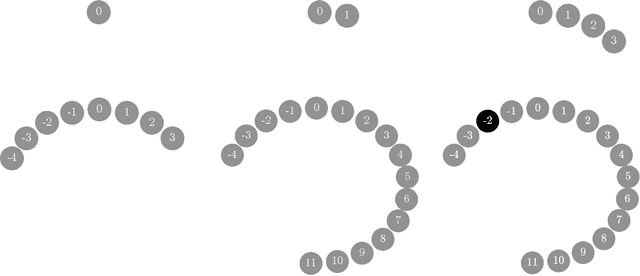
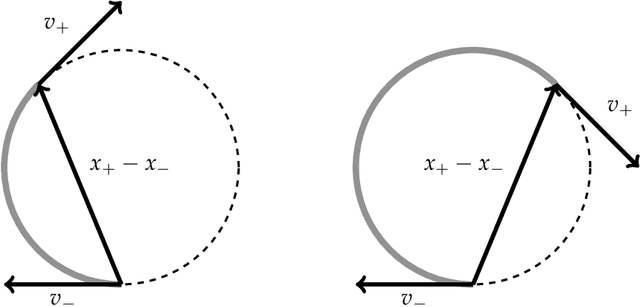
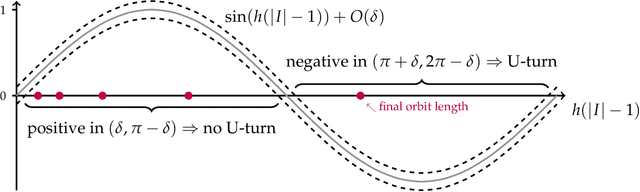
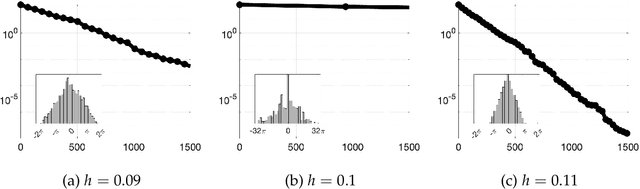
We prove that the mixing time of the No-U-Turn Sampler (NUTS), when initialized in the concentration region of the canonical Gaussian measure, scales as $d^{1/4}$, up to logarithmic factors, where $d$ is the dimension. This scaling is expected to be sharp. This result is based on a coupling argument that leverages the geometric structure of the target distribution. Specifically, concentration of measure results in a striking uniformity in NUTS' locally adapted transitions, which holds with high probability. This uniformity is formalized by interpreting NUTS as an accept/reject Markov chain, where the mixing properties for the more uniform accept chain are analytically tractable. Additionally, our analysis uncovers a previously unnoticed issue with the path length adaptation procedure of NUTS, specifically related to looping behavior, which we address in detail.