Modelling local and global phenomena with sparse Gaussian processes
Paper and Code
Jun 13, 2012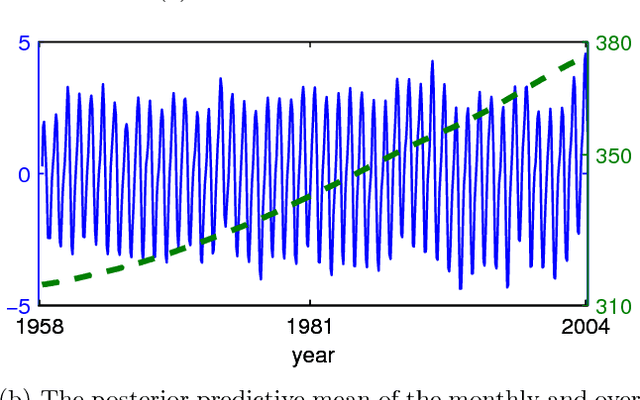
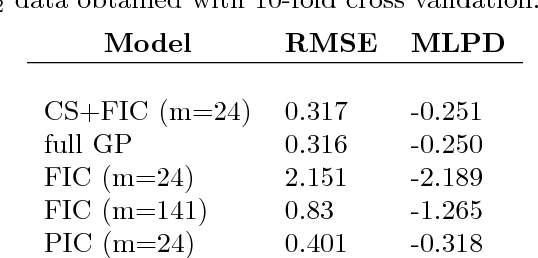


Much recent work has concerned sparse approximations to speed up the Gaussian process regression from the unfavorable O(n3) scaling in computational time to O(nm2). Thus far, work has concentrated on models with one covariance function. However, in many practical situations additive models with multiple covariance functions may perform better, since the data may contain both long and short length-scale phenomena. The long length-scales can be captured with global sparse approximations, such as fully independent conditional (FIC), and the short length-scales can be modeled naturally by covariance functions with compact support (CS). CS covariance functions lead to naturally sparse covariance matrices, which are computationally cheaper to handle than full covariance matrices. In this paper, we propose a new sparse Gaussian process model with two additive components: FIC for the long length-scales and CS covariance function for the short length-scales. We give theoretical and experimental results and show that under certain conditions the proposed model has the same computational complexity as FIC. We also compare the model performance of the proposed model to additive models approximated by fully and partially independent conditional (PIC). We use real data sets and show that our model outperforms FIC and PIC approximations for data sets with two additive phenomena.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge