Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models

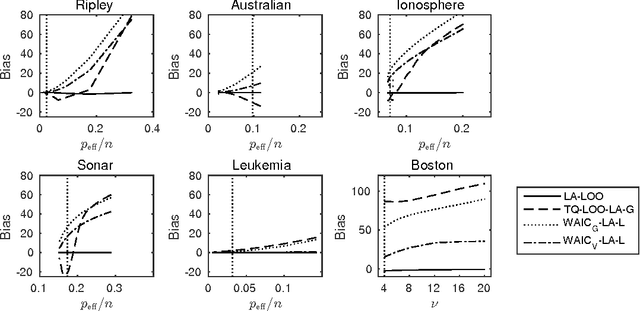
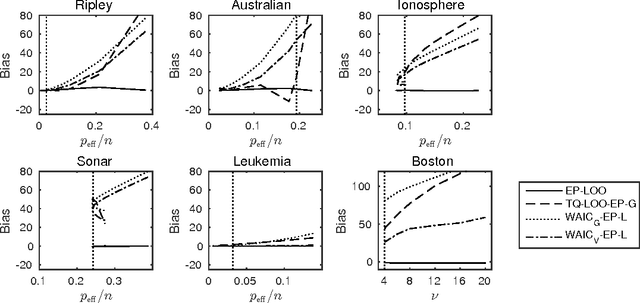
The future predictive performance of a Bayesian model can be estimated using Bayesian cross-validation. In this article, we consider Gaussian latent variable models where the integration over the latent values is approximated using the Laplace method or expectation propagation (EP). We study the properties of several Bayesian leave-one-out (LOO) cross-validation approximations that in most cases can be computed with a small additional cost after forming the posterior approximation given the full data. Our main objective is to assess the accuracy of the approximative LOO cross-validation estimators. That is, for each method (Laplace and EP) we compare the approximate fast computation with the exact brute force LOO computation. Secondarily, we evaluate the accuracy of the Laplace and EP approximations themselves against a ground truth established through extensive Markov chain Monte Carlo simulation. Our empirical results show that the approach based upon a Gaussian approximation to the LOO marginal distribution (the so-called cavity distribution) gives the most accurate and reliable results among the fast methods.

Bayesian Modeling with Gaussian Processes using the GPstuff Toolbox

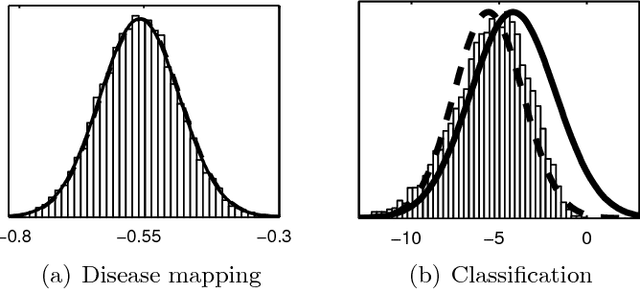
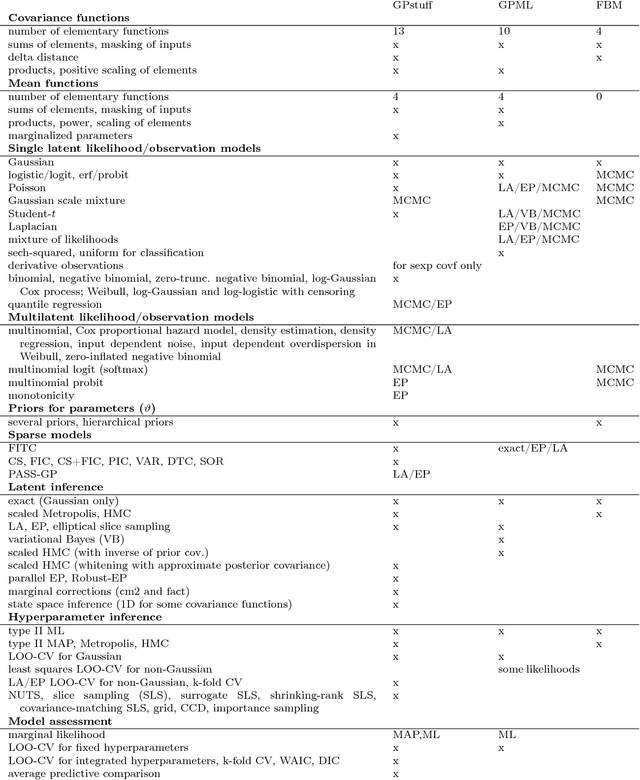
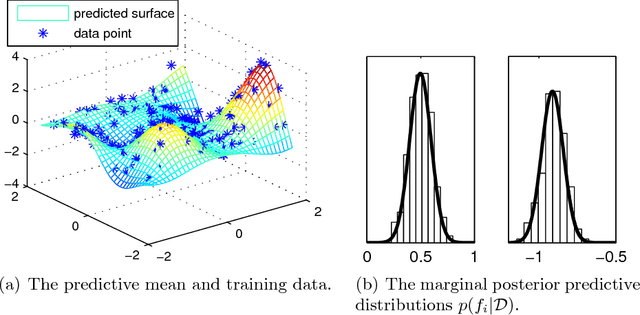
Gaussian processes (GP) are powerful tools for probabilistic modeling purposes. They can be used to define prior distributions over latent functions in hierarchical Bayesian models. The prior over functions is defined implicitly by the mean and covariance function, which determine the smoothness and variability of the function. The inference can then be conducted directly in the function space by evaluating or approximating the posterior process. Despite their attractive theoretical properties GPs provide practical challenges in their implementation. GPstuff is a versatile collection of computational tools for GP models compatible with Linux and Windows MATLAB and Octave. It includes, among others, various inference methods, sparse approximations and tools for model assessment. In this work, we review these tools and demonstrate the use of GPstuff in several models.

Approximate Inference for Nonstationary Heteroscedastic Gaussian process Regression

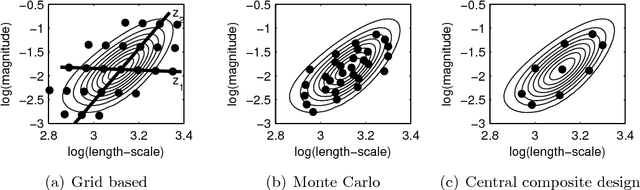
This paper presents a novel approach for approximate integration over the uncertainty of noise and signal variances in Gaussian process (GP) regression. Our efficient and straightforward approach can also be applied to integration over input dependent noise variance (heteroscedasticity) and input dependent signal variance (nonstationarity) by setting independent GP priors for the noise and signal variances. We use expectation propagation (EP) for inference and compare results to Markov chain Monte Carlo in two simulated data sets and three empirical examples. The results show that EP produces comparable results with less computational burden.