Bayesian Modeling with Gaussian Processes using the GPstuff Toolbox

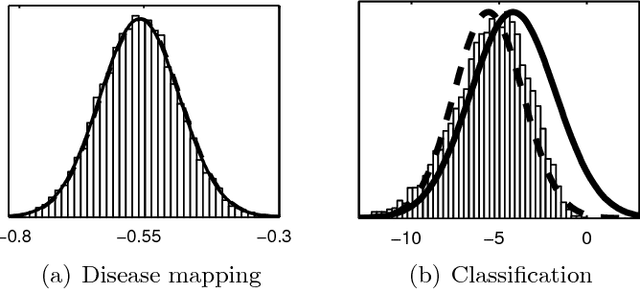
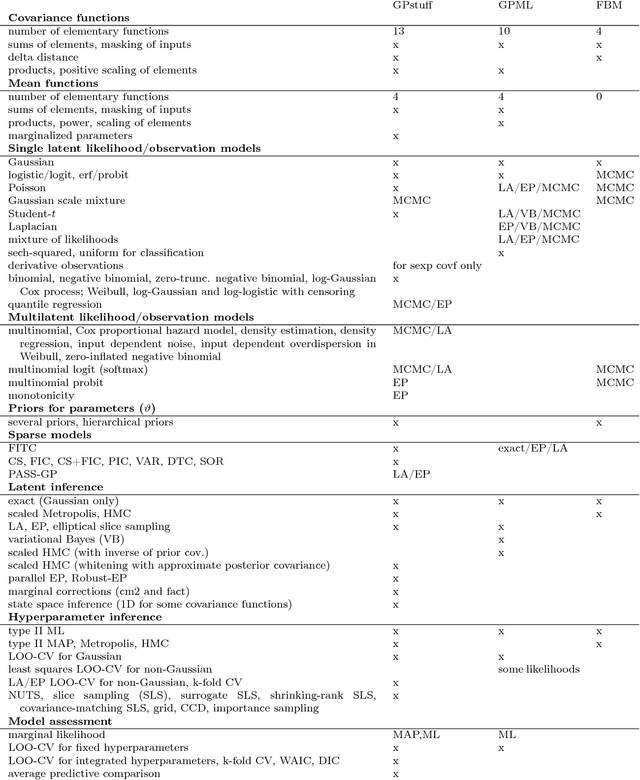
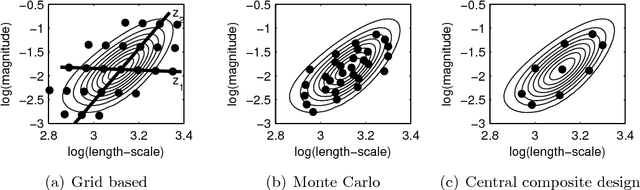
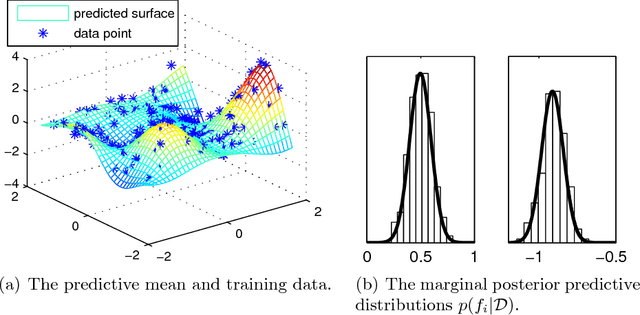
Gaussian processes (GP) are powerful tools for probabilistic modeling purposes. They can be used to define prior distributions over latent functions in hierarchical Bayesian models. The prior over functions is defined implicitly by the mean and covariance function, which determine the smoothness and variability of the function. The inference can then be conducted directly in the function space by evaluating or approximating the posterior process. Despite their attractive theoretical properties GPs provide practical challenges in their implementation. GPstuff is a versatile collection of computational tools for GP models compatible with Linux and Windows MATLAB and Octave. It includes, among others, various inference methods, sparse approximations and tools for model assessment. In this work, we review these tools and demonstrate the use of GPstuff in several models.

On the relation between Gaussian process quadratures and sigma-point methods

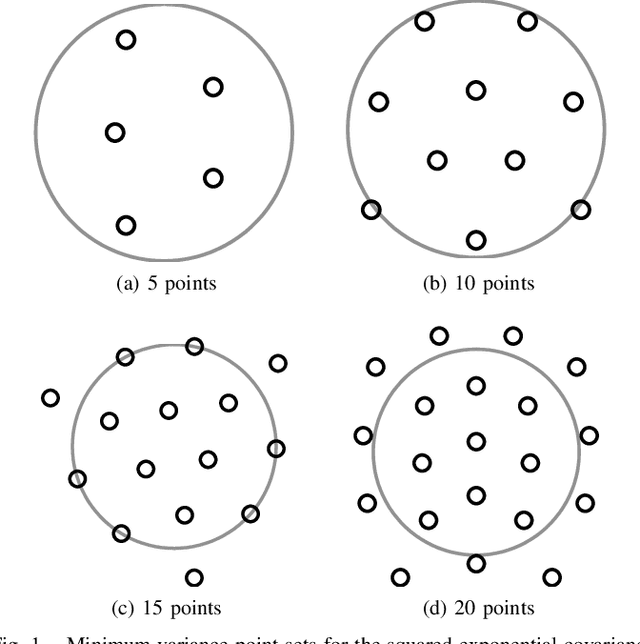
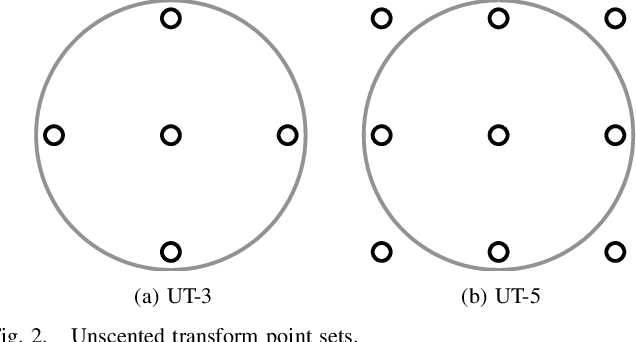
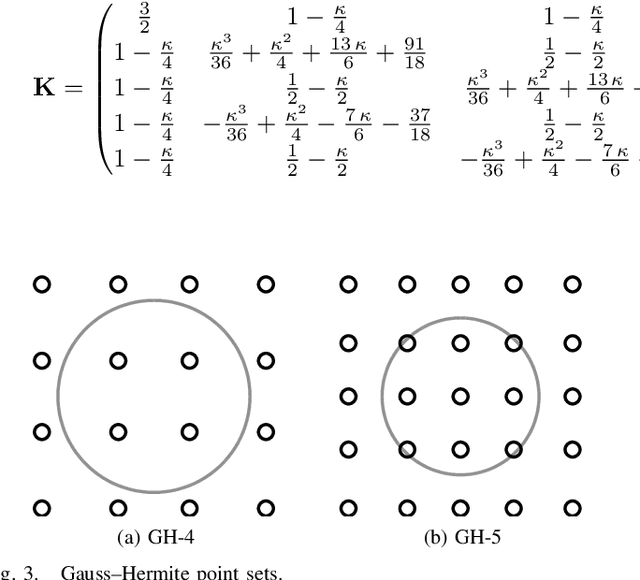
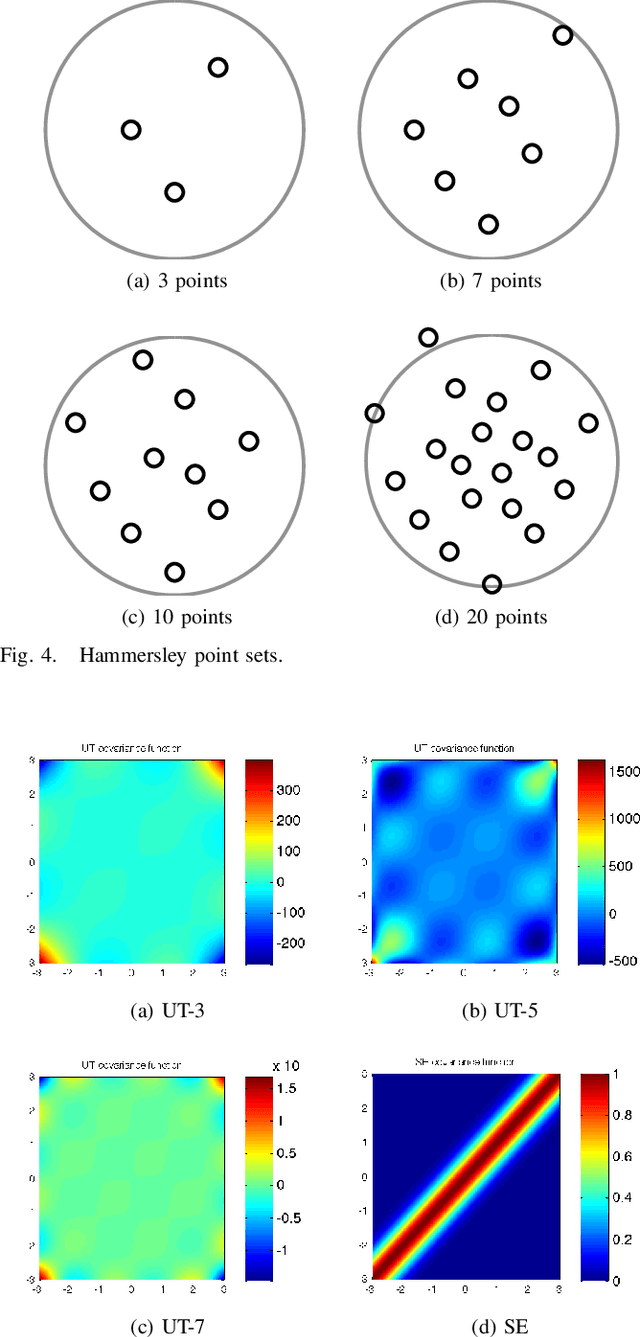
This article is concerned with Gaussian process quadratures, which are numerical integration methods based on Gaussian process regression methods, and sigma-point methods, which are used in advanced non-linear Kalman filtering and smoothing algorithms. We show that many sigma-point methods can be interpreted as Gaussian quadrature based methods with suitably selected covariance functions. We show that this interpretation also extends to more general multivariate Gauss--Hermite integration methods and related spherical cubature rules. Additionally, we discuss different criteria for selecting the sigma-point locations: exactness for multivariate polynomials up to a given order, minimum average error, and quasi-random point sets. The performance of the different methods is tested in numerical experiments.

State-Space Inference for Non-Linear Latent Force Models with Application to Satellite Orbit Prediction

Latent force models (LFMs) are flexible models that combine mechanistic modelling principles (i.e., physical models) with non-parametric data-driven components. Several key applications of LFMs need non-linearities, which results in analytically intractable inference. In this work we show how non-linear LFMs can be represented as non-linear white noise driven state-space models and present an efficient non-linear Kalman filtering and smoothing based method for approximate state and parameter inference. We illustrate the performance of the proposed methodology via two simulated examples, and apply it to a real-world problem of long-term prediction of GPS satellite orbits.

Sequential Inference for Latent Force Models

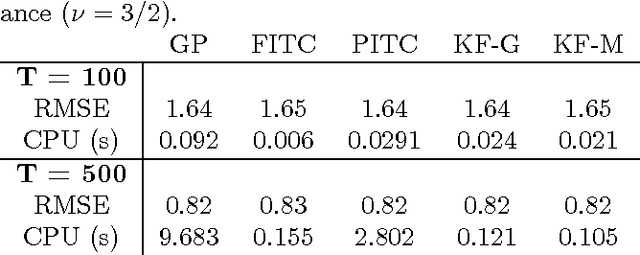
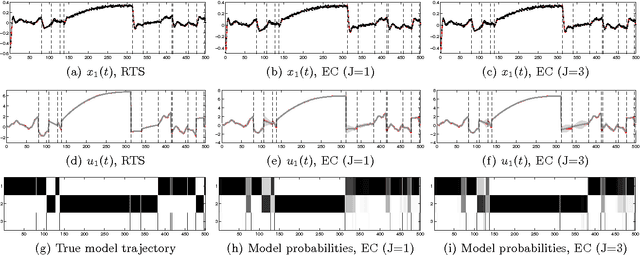
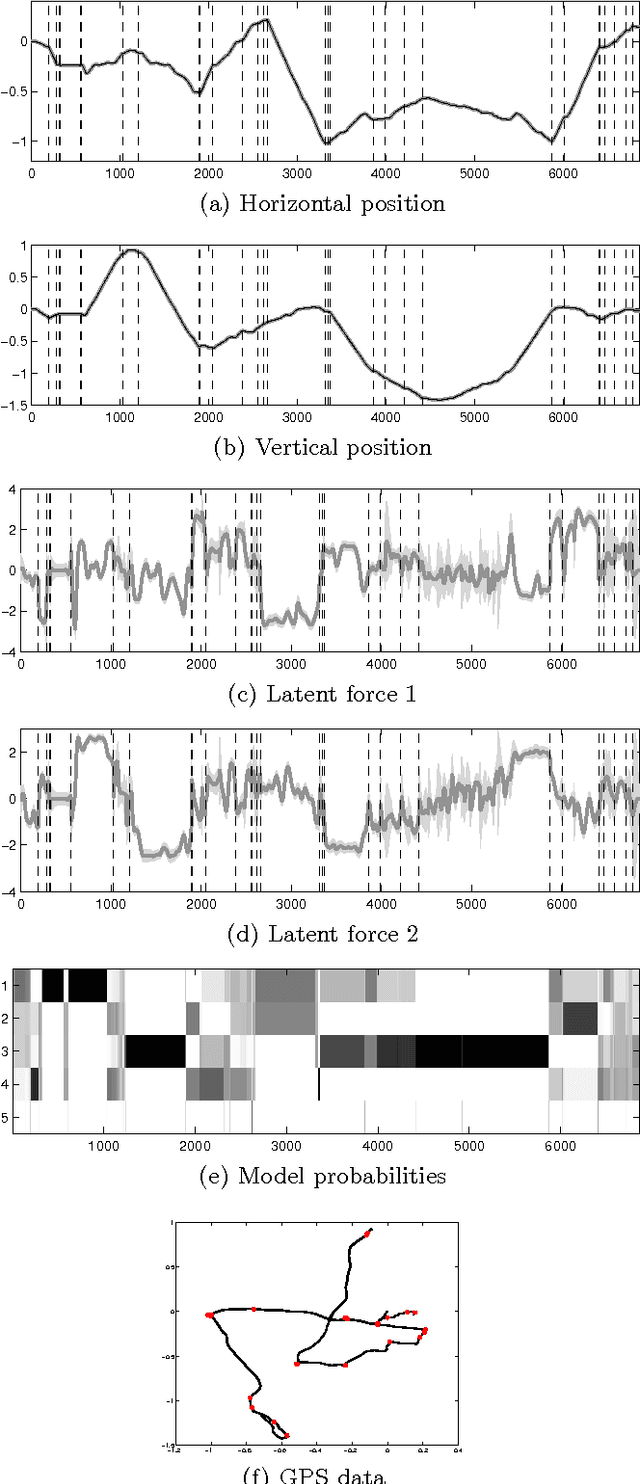
Latent force models (LFMs) are hybrid models combining mechanistic principles with non-parametric components. In this article, we shall show how LFMs can be equivalently formulated and solved using the state variable approach. We shall also show how the Gaussian process prior used in LFMs can be equivalently formulated as a linear statespace model driven by a white noise process and how inference on the resulting model can be efficiently implemented using Kalman filter and smoother. Then we shall show how the recently proposed switching LFM can be reformulated using the state variable approach, and how we can construct a probabilistic model for the switches by formulating a similar switching LFM as a switching linear dynamic system (SLDS). We illustrate the performance of the proposed methodology in simulated scenarios and apply it to inferring the switching points in GPS data collected from car movement data in urban environment.