Sequential Inference for Latent Force Models
Paper and Code
Feb 14, 2012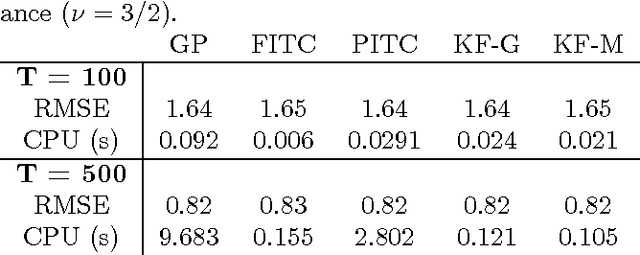
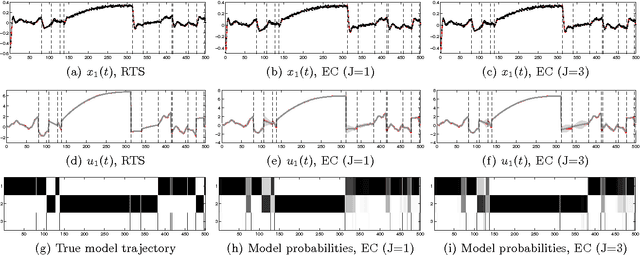
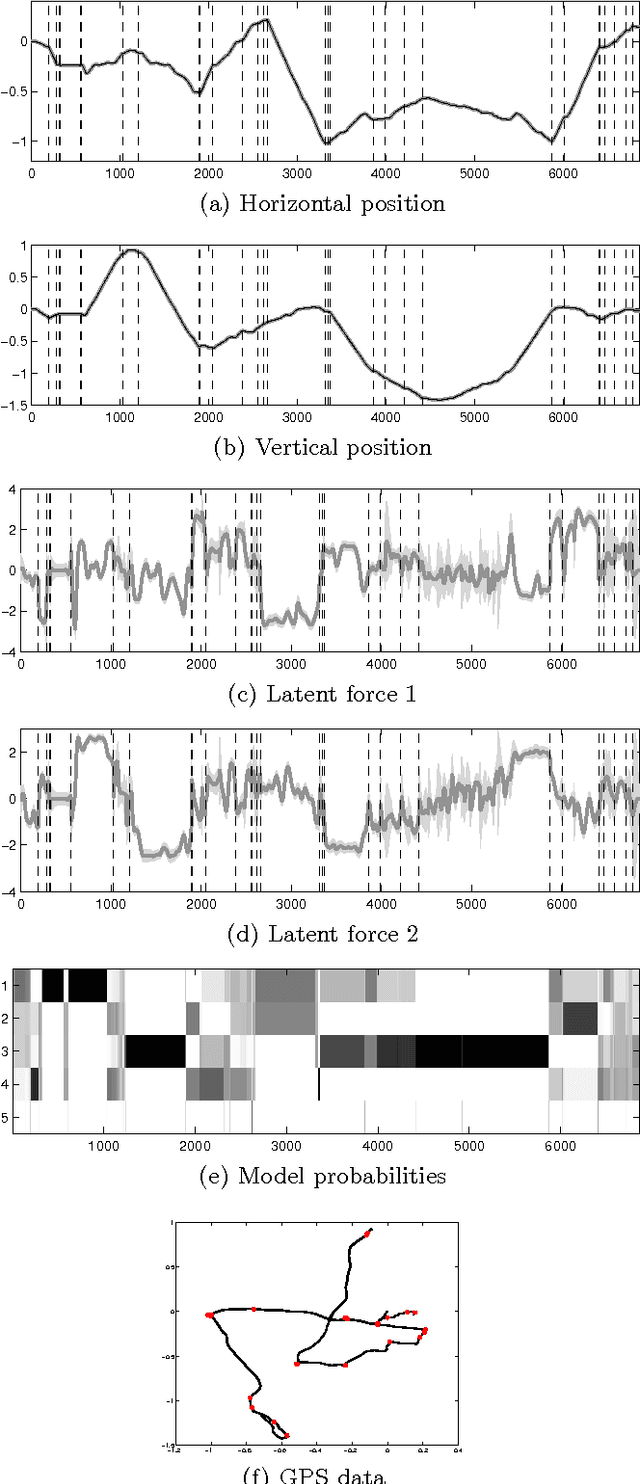
Latent force models (LFMs) are hybrid models combining mechanistic principles with non-parametric components. In this article, we shall show how LFMs can be equivalently formulated and solved using the state variable approach. We shall also show how the Gaussian process prior used in LFMs can be equivalently formulated as a linear statespace model driven by a white noise process and how inference on the resulting model can be efficiently implemented using Kalman filter and smoother. Then we shall show how the recently proposed switching LFM can be reformulated using the state variable approach, and how we can construct a probabilistic model for the switches by formulating a similar switching LFM as a switching linear dynamic system (SLDS). We illustrate the performance of the proposed methodology in simulated scenarios and apply it to inferring the switching points in GPS data collected from car movement data in urban environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge