Bayesian Modeling with Gaussian Processes using the GPstuff Toolbox

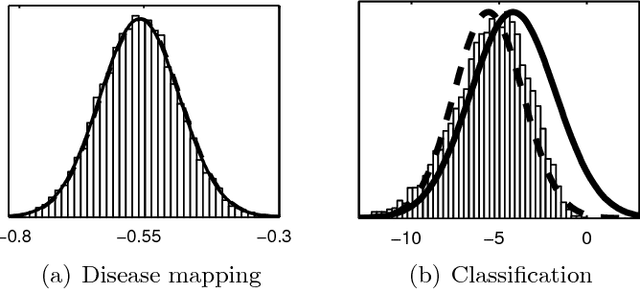
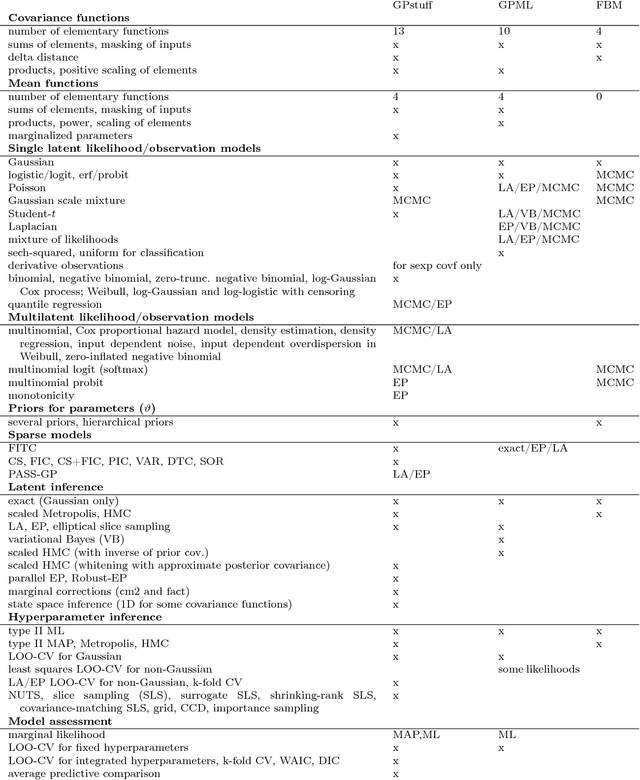
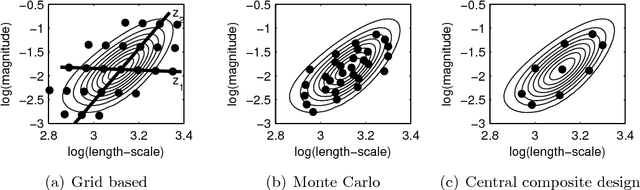
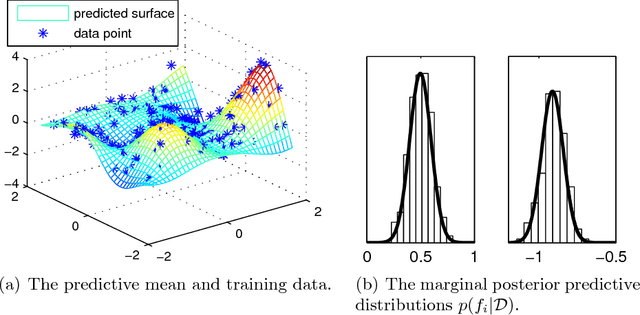
Gaussian processes (GP) are powerful tools for probabilistic modeling purposes. They can be used to define prior distributions over latent functions in hierarchical Bayesian models. The prior over functions is defined implicitly by the mean and covariance function, which determine the smoothness and variability of the function. The inference can then be conducted directly in the function space by evaluating or approximating the posterior process. Despite their attractive theoretical properties GPs provide practical challenges in their implementation. GPstuff is a versatile collection of computational tools for GP models compatible with Linux and Windows MATLAB and Octave. It includes, among others, various inference methods, sparse approximations and tools for model assessment. In this work, we review these tools and demonstrate the use of GPstuff in several models.

Laplace approximation for logistic Gaussian process density estimation and regression

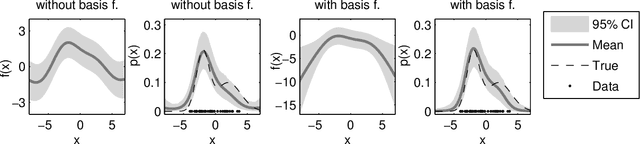
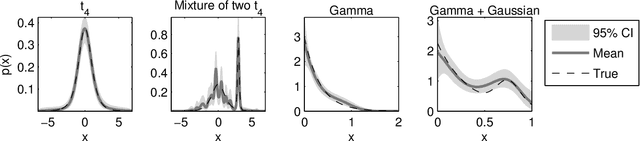
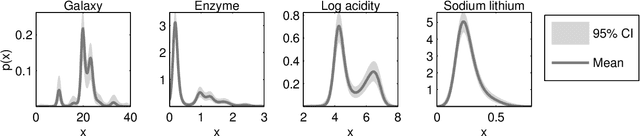
Logistic Gaussian process (LGP) priors provide a flexible alternative for modelling unknown densities. The smoothness properties of the density estimates can be controlled through the prior covariance structure of the LGP, but the challenge is the analytically intractable inference. In this paper, we present approximate Bayesian inference for LGP density estimation in a grid using Laplace's method to integrate over the non-Gaussian posterior distribution of latent function values and to determine the covariance function parameters with type-II maximum a posteriori (MAP) estimation. We demonstrate that Laplace's method with MAP is sufficiently fast for practical interactive visualisation of 1D and 2D densities. Our experiments with simulated and real 1D data sets show that the estimation accuracy is close to a Markov chain Monte Carlo approximation and state-of-the-art hierarchical infinite Gaussian mixture models. We also construct a reduced-rank approximation to speed up the computations for dense 2D grids, and demonstrate density regression with the proposed Laplace approach.

Nested Expectation Propagation for Gaussian Process Classification with a Multinomial Probit Likelihood

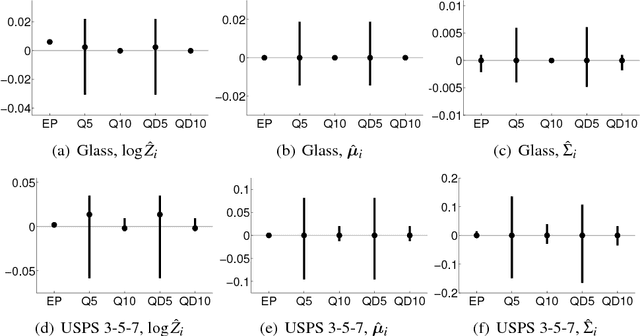
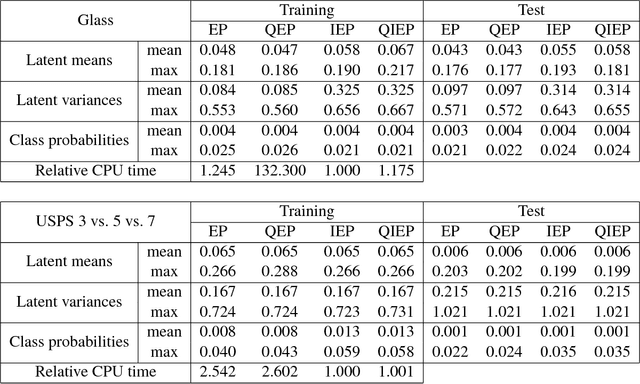
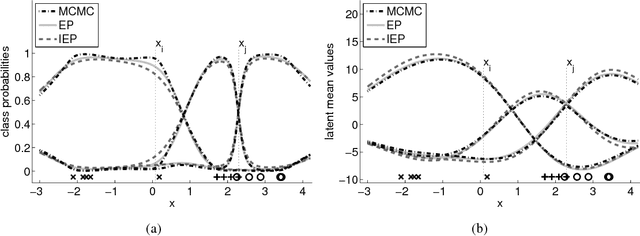
We consider probabilistic multinomial probit classification using Gaussian process (GP) priors. The challenges with the multiclass GP classification are the integration over the non-Gaussian posterior distribution, and the increase of the number of unknown latent variables as the number of target classes grows. Expectation propagation (EP) has proven to be a very accurate method for approximate inference but the existing EP approaches for the multinomial probit GP classification rely on numerical quadratures or independence assumptions between the latent values from different classes to facilitate the computations. In this paper, we propose a novel nested EP approach which does not require numerical quadratures, and approximates accurately all between-class posterior dependencies of the latent values, but still scales linearly in the number of classes. The predictive accuracy of the nested EP approach is compared to Laplace, variational Bayes, and Markov chain Monte Carlo (MCMC) approximations with various benchmark data sets. In the experiments nested EP was the most consistent method with respect to MCMC sampling, but the differences between the compared methods were small if only the classification accuracy is concerned.