A multi-modal dataset for insect biodiversity with imagery and DNA at the trap and individual level

Insects comprise millions of species, many experiencing severe population declines under environmental and habitat changes. High-throughput approaches are crucial for accelerating our understanding of insect diversity, with DNA barcoding and high-resolution imaging showing strong potential for automatic taxonomic classification. However, most image-based approaches rely on individual specimen data, unlike the unsorted bulk samples collected in large-scale ecological surveys. We present the Mixed Arthropod Sample Segmentation and Identification (MassID45) dataset for training automatic classifiers of bulk insect samples. It uniquely combines molecular and imaging data at both the unsorted sample level and the full set of individual specimens. Human annotators, supported by an AI-assisted tool, performed two tasks on bulk images: creating segmentation masks around each individual arthropod and assigning taxonomic labels to over 17 000 specimens. Combining the taxonomic resolution of DNA barcodes with precise abundance estimates of bulk images holds great potential for rapid, large-scale characterization of insect communities. This dataset pushes the boundaries of tiny object detection and instance segmentation, fostering innovation in both ecological and machine learning research.

Classification of weak multi-view signals by sharing factors in a mixture of Bayesian group factor analyzers

We propose a novel classification model for weak signal data, building upon a recent model for Bayesian multi-view learning, Group Factor Analysis (GFA). Instead of assuming all data to come from a single GFA model, we allow latent clusters, each having a different GFA model and producing a different class distribution. We show that sharing information across the clusters, by sharing factors, increases the classification accuracy considerably; the shared factors essentially form a flexible noise model that explains away the part of data not related to classification. Motivation for the setting comes from single-trial functional brain imaging data, having a very low signal-to-noise ratio and a natural multi-view setting, with the different sensors, measurement modalities (EEG, MEG, fMRI) and possible auxiliary information as views. We demonstrate our model on a MEG dataset.

Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models

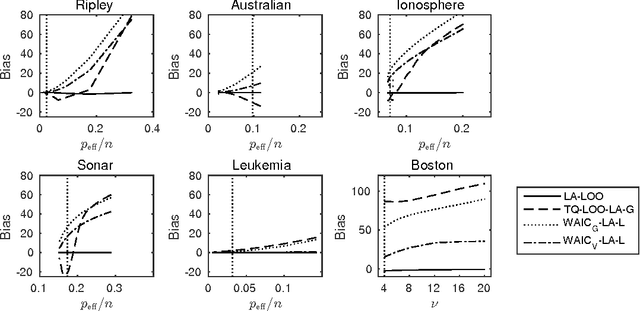
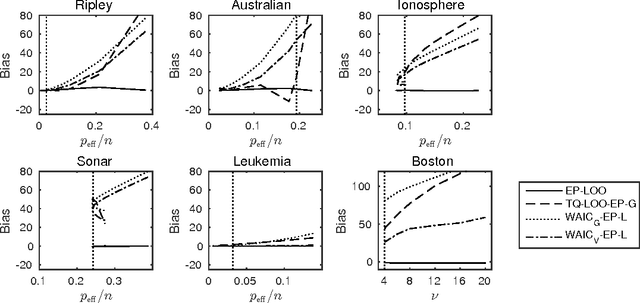
The future predictive performance of a Bayesian model can be estimated using Bayesian cross-validation. In this article, we consider Gaussian latent variable models where the integration over the latent values is approximated using the Laplace method or expectation propagation (EP). We study the properties of several Bayesian leave-one-out (LOO) cross-validation approximations that in most cases can be computed with a small additional cost after forming the posterior approximation given the full data. Our main objective is to assess the accuracy of the approximative LOO cross-validation estimators. That is, for each method (Laplace and EP) we compare the approximate fast computation with the exact brute force LOO computation. Secondarily, we evaluate the accuracy of the Laplace and EP approximations themselves against a ground truth established through extensive Markov chain Monte Carlo simulation. Our empirical results show that the approach based upon a Gaussian approximation to the LOO marginal distribution (the so-called cavity distribution) gives the most accurate and reliable results among the fast methods.