Neural Non-Stationary Spectral Kernel

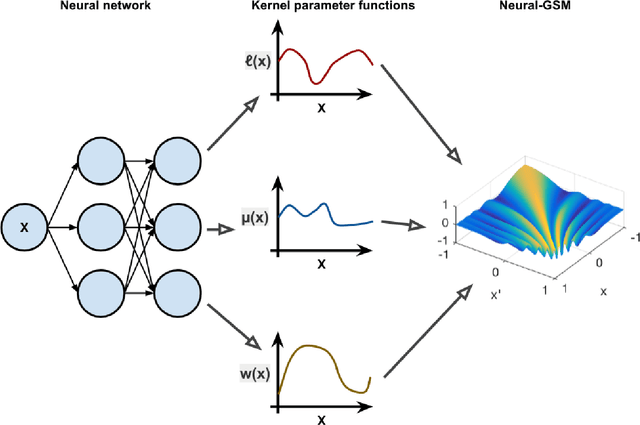
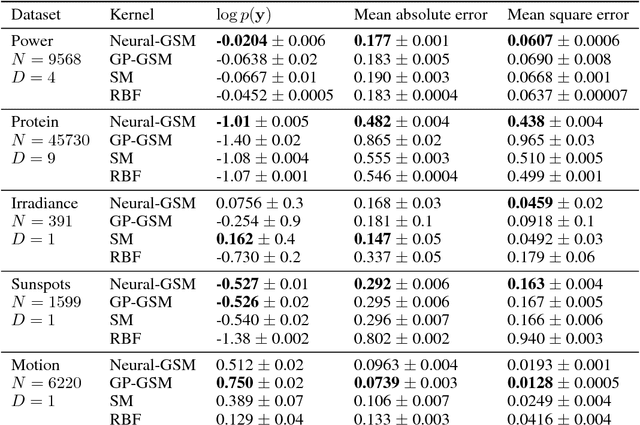
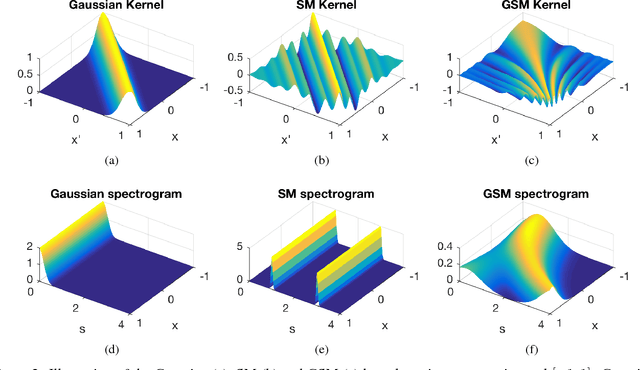
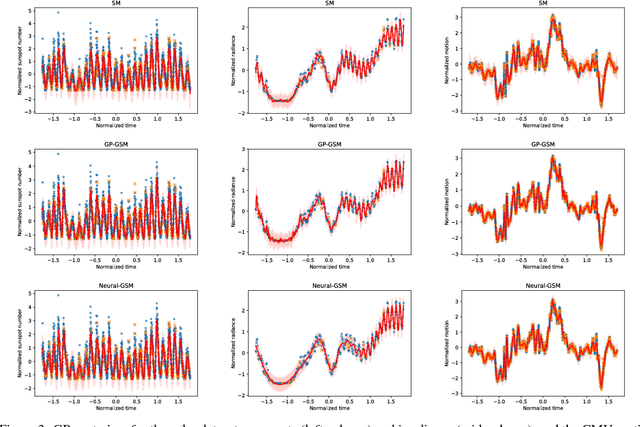
Standard kernels such as Mat\'ern or RBF kernels only encode simple monotonic dependencies within the input space. Spectral mixture kernels have been proposed as general-purpose, flexible kernels for learning and discovering more complicated patterns in the data. Spectral mixture kernels have recently been generalized into non-stationary kernels by replacing the mixture weights, frequency means and variances by input-dependent functions. These functions have also been modelled as Gaussian processes on their own. In this paper we propose modelling the hyperparameter functions with neural networks, and provide an experimental comparison between the stationary spectral mixture and the two non-stationary spectral mixtures. Scalable Gaussian process inference is implemented within the sparse variational framework for all the kernels considered. We show that the neural variant of the kernel is able to achieve the best performance, among alternatives, on several benchmark datasets.

A Mutually-Dependent Hadamard Kernel for Modelling Latent Variable Couplings

We introduce a novel kernel that models input-dependent couplings across multiple latent processes. The pairwise joint kernel measures covariance along inputs and across different latent signals in a mutually-dependent fashion. A latent correlation Gaussian process (LCGP) model combines these non-stationary latent components into multiple outputs by an input-dependent mixing matrix. Probit classification and support for multiple observation sets are derived by Variational Bayesian inference. Results on several datasets indicate that the LCGP model can recover the correlations between latent signals while simultaneously achieving state-of-the-art performance. We highlight the latent covariances with an EEG classification dataset where latent brain processes and their couplings simultaneously emerge from the model.

Non-Stationary Spectral Kernels

We propose non-stationary spectral kernels for Gaussian process regression. We propose to model the spectral density of a non-stationary kernel function as a mixture of input-dependent Gaussian process frequency density surfaces. We solve the generalised Fourier transform with such a model, and present a family of non-stationary and non-monotonic kernels that can learn input-dependent and potentially long-range, non-monotonic covariances between inputs. We derive efficient inference using model whitening and marginalized posterior, and show with case studies that these kernels are necessary when modelling even rather simple time series, image or geospatial data with non-stationary characteristics.

Classification of weak multi-view signals by sharing factors in a mixture of Bayesian group factor analyzers

We propose a novel classification model for weak signal data, building upon a recent model for Bayesian multi-view learning, Group Factor Analysis (GFA). Instead of assuming all data to come from a single GFA model, we allow latent clusters, each having a different GFA model and producing a different class distribution. We show that sharing information across the clusters, by sharing factors, increases the classification accuracy considerably; the shared factors essentially form a flexible noise model that explains away the part of data not related to classification. Motivation for the setting comes from single-trial functional brain imaging data, having a very low signal-to-noise ratio and a natural multi-view setting, with the different sensors, measurement modalities (EEG, MEG, fMRI) and possible auxiliary information as views. We demonstrate our model on a MEG dataset.