Neural Non-Stationary Spectral Kernel
Paper and Code
Nov 27, 2018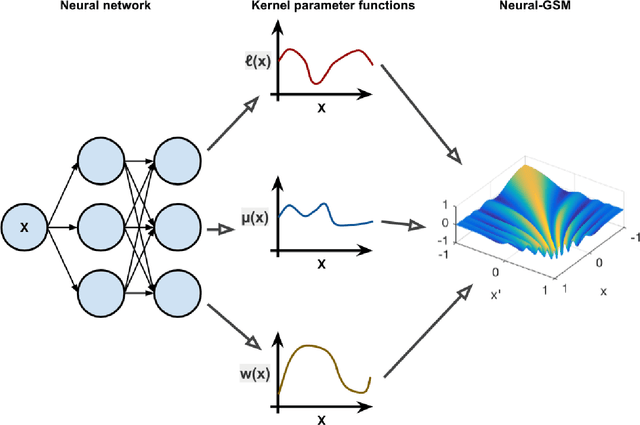
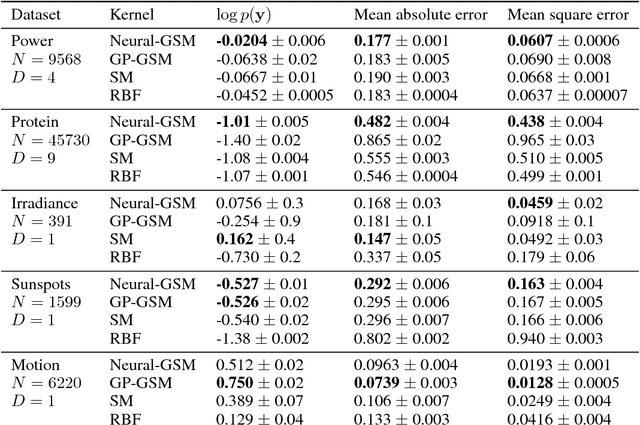
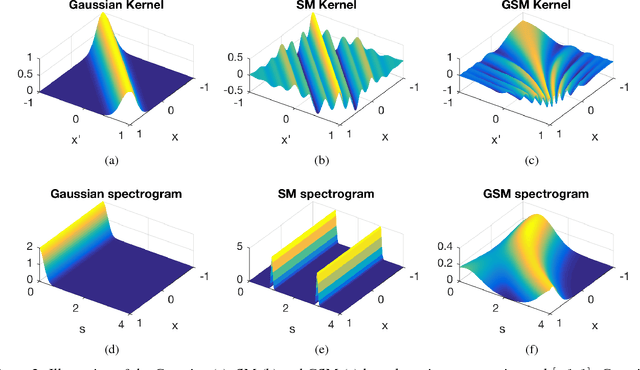
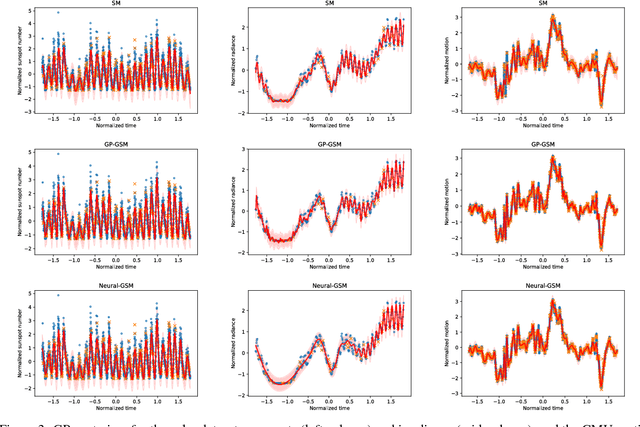
Standard kernels such as Mat\'ern or RBF kernels only encode simple monotonic dependencies within the input space. Spectral mixture kernels have been proposed as general-purpose, flexible kernels for learning and discovering more complicated patterns in the data. Spectral mixture kernels have recently been generalized into non-stationary kernels by replacing the mixture weights, frequency means and variances by input-dependent functions. These functions have also been modelled as Gaussian processes on their own. In this paper we propose modelling the hyperparameter functions with neural networks, and provide an experimental comparison between the stationary spectral mixture and the two non-stationary spectral mixtures. Scalable Gaussian process inference is implemented within the sparse variational framework for all the kernels considered. We show that the neural variant of the kernel is able to achieve the best performance, among alternatives, on several benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge