Population Empirical Bayes
Paper and Code
Jun 08, 2015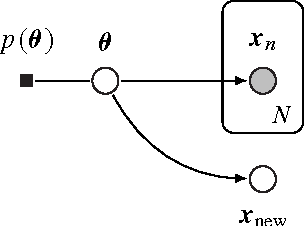
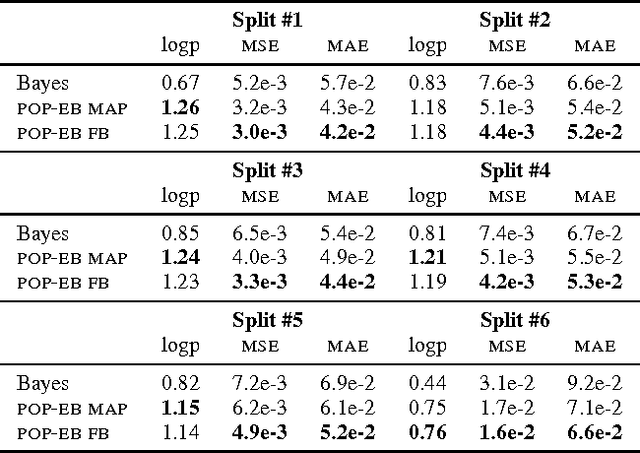
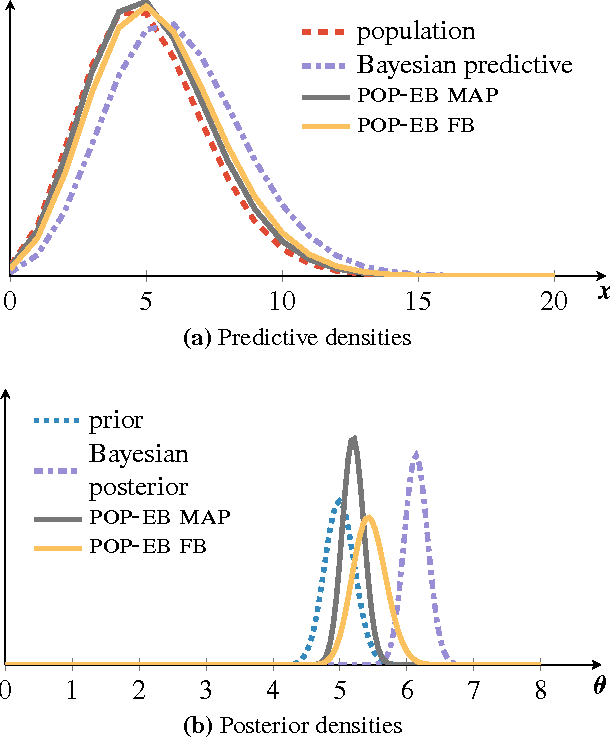
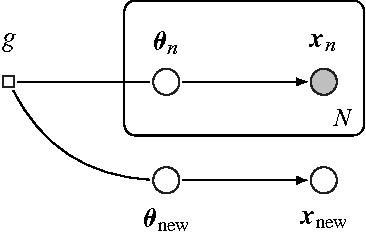
Bayesian predictive inference analyzes a dataset to make predictions about new observations. When a model does not match the data, predictive accuracy suffers. We develop population empirical Bayes (POP-EB), a hierarchical framework that explicitly models the empirical population distribution as part of Bayesian analysis. We introduce a new concept, the latent dataset, as a hierarchical variable and set the empirical population as its prior. This leads to a new predictive density that mitigates model mismatch. We efficiently apply this method to complex models by proposing a stochastic variational inference algorithm, called bumping variational inference (BUMP-VI). We demonstrate improved predictive accuracy over classical Bayesian inference in three models: a linear regression model of health data, a Bayesian mixture model of natural images, and a latent Dirichlet allocation topic model of scientific documents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge