Posterior Dispersion Indices
Paper and Code
May 24, 2016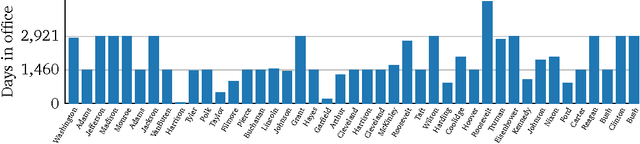
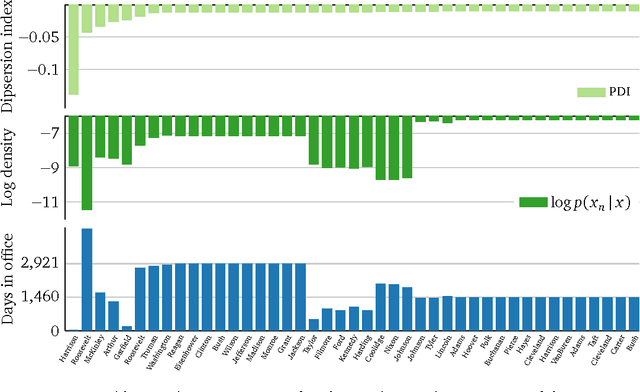

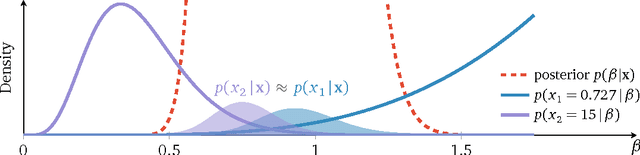
Probabilistic modeling is cyclical: we specify a model, infer its posterior, and evaluate its performance. Evaluation drives the cycle, as we revise our model based on how it performs. This requires a metric. Traditionally, predictive accuracy prevails. Yet, predictive accuracy does not tell the whole story. We propose to evaluate a model through posterior dispersion. The idea is to analyze how each datapoint fares in relation to posterior uncertainty around the hidden structure. We propose a family of posterior dispersion indices (PDI) that capture this idea. A PDI identifies rich patterns of model mismatch in three real data examples: voting preferences, supermarket shopping, and population genetics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge