Covariance Matrices for Mean Field Variational Bayes
Paper and Code
Dec 08, 2014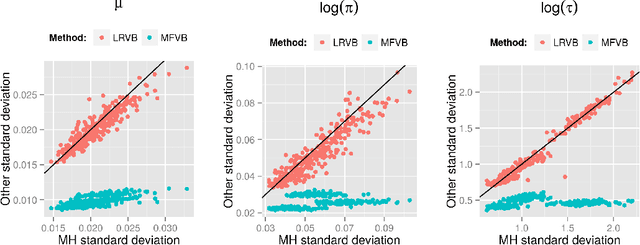
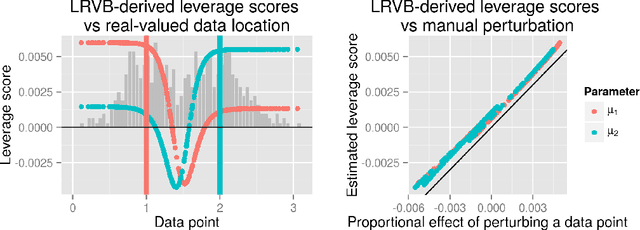
Mean Field Variational Bayes (MFVB) is a popular posterior approximation method due to its fast runtime on large-scale data sets. However, it is well known that a major failing of MFVB is its (sometimes severe) underestimates of the uncertainty of model variables and lack of information about model variable covariance. We develop a fast, general methodology for exponential families that augments MFVB to deliver accurate uncertainty estimates for model variables -- both for individual variables and coherently across variables. MFVB for exponential families defines a fixed-point equation in the means of the approximating posterior, and our approach yields a covariance estimate by perturbing this fixed point. Inspired by linear response theory, we call our method linear response variational Bayes (LRVB). We demonstrate the accuracy of our method on simulated data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge