Alessandro Davide Ialongo
Evaluating model-based planning and planner amortization for continuous control
Oct 07, 2021
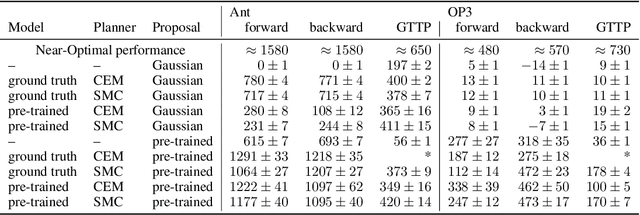
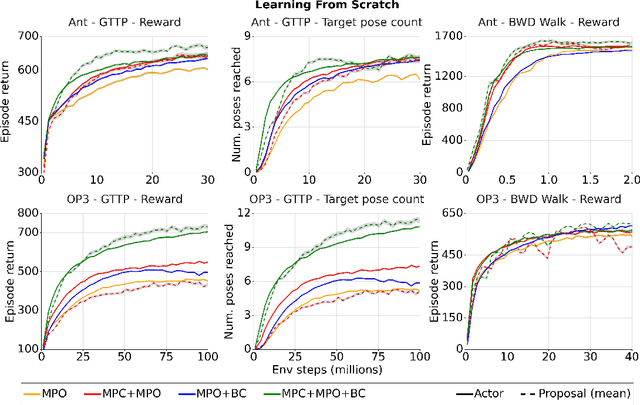
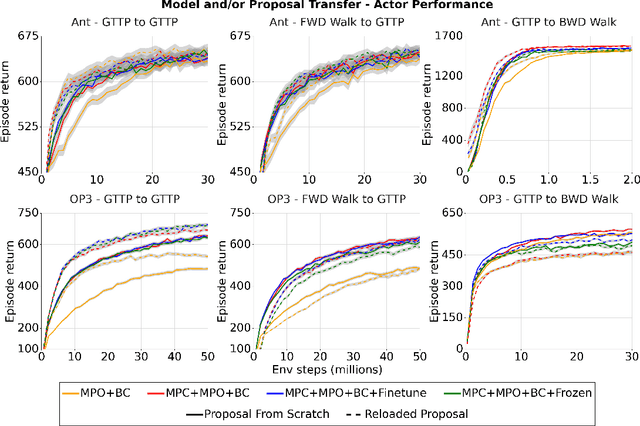
Abstract:There is a widespread intuition that model-based control methods should be able to surpass the data efficiency of model-free approaches. In this paper we attempt to evaluate this intuition on various challenging locomotion tasks. We take a hybrid approach, combining model predictive control (MPC) with a learned model and model-free policy learning; the learned policy serves as a proposal for MPC. We find that well-tuned model-free agents are strong baselines even for high DoF control problems but MPC with learned proposals and models (trained on the fly or transferred from related tasks) can significantly improve performance and data efficiency in hard multi-task/multi-goal settings. Finally, we show that it is possible to distil a model-based planner into a policy that amortizes the planning computation without any loss of performance. Videos of agents performing different tasks can be seen at https://sites.google.com/view/mbrl-amortization/home.
Iterative Amortized Policy Optimization
Oct 20, 2020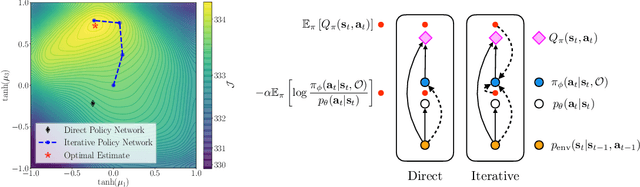
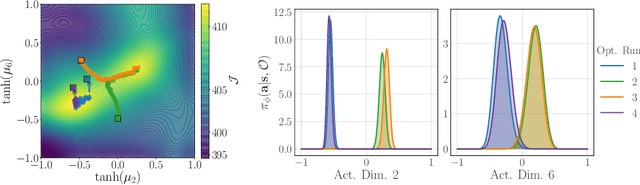
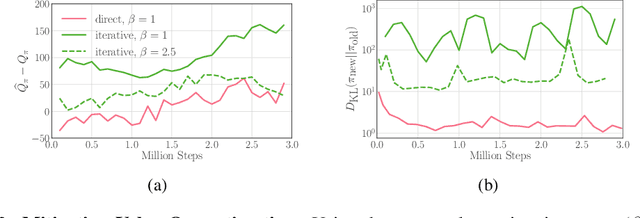
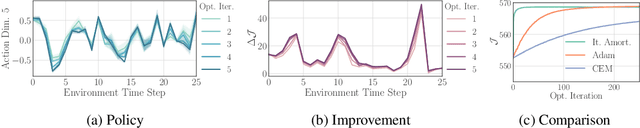
Abstract:Policy networks are a central feature of deep reinforcement learning (RL) algorithms for continuous control, enabling the estimation and sampling of high-value actions. From the variational inference perspective on RL, policy networks, when employed with entropy or KL regularization, are a form of amortized optimization, optimizing network parameters rather than the policy distributions directly. However, this direct amortized mapping can empirically yield suboptimal policy estimates. Given this perspective, we consider the more flexible class of iterative amortized optimizers. We demonstrate that the resulting technique, iterative amortized policy optimization, yields performance improvements over conventional direct amortization methods on benchmark continuous control tasks.
Overcoming Mean-Field Approximations in Recurrent Gaussian Process Models
Jun 13, 2019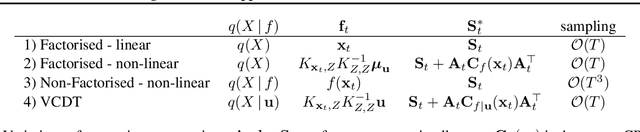
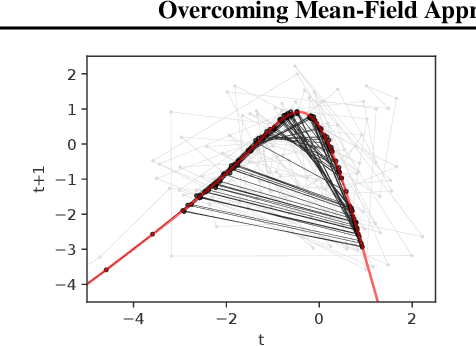
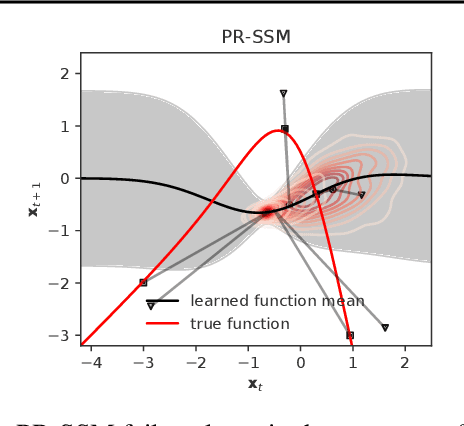

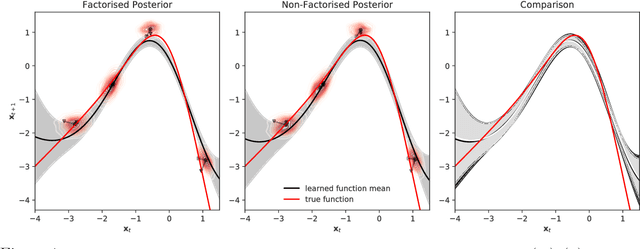
Abstract:We identify a new variational inference scheme for dynamical systems whose transition function is modelled by a Gaussian process. Inference in this setting has either employed computationally intensive MCMC methods, or relied on factorisations of the variational posterior. As we demonstrate in our experiments, the factorisation between latent system states and transition function can lead to a miscalibrated posterior and to learning unnecessarily large noise terms. We eliminate this factorisation by explicitly modelling the dependence between state trajectories and the Gaussian process posterior. Samples of the latent states can then be tractably generated by conditioning on this representation. The method we obtain (VCDT: variationally coupled dynamics and trajectories) gives better predictive performance and more calibrated estimates of the transition function, yet maintains the same time and space complexities as mean-field methods. Code is available at: github.com/ialong/GPt.
* 10 pages, 4 figures, 3 tables. Published in the proceedings of the Thirty-sixth International Conference on Machine Learning (ICML), 2019
Non-Factorised Variational Inference in Dynamical Systems
Dec 14, 2018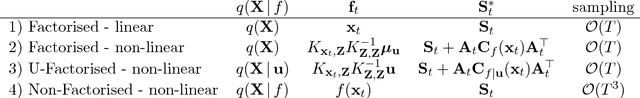
Abstract:We focus on variational inference in dynamical systems where the discrete time transition function (or evolution rule) is modelled by a Gaussian process. The dominant approach so far has been to use a factorised posterior distribution, decoupling the transition function from the system states. This is not exact in general and can lead to an overconfident posterior over the transition function as well as an overestimation of the intrinsic stochasticity of the system (process noise). We propose a new method that addresses these issues and incurs no additional computational costs.
Closed-form Inference and Prediction in Gaussian Process State-Space Models
Dec 10, 2018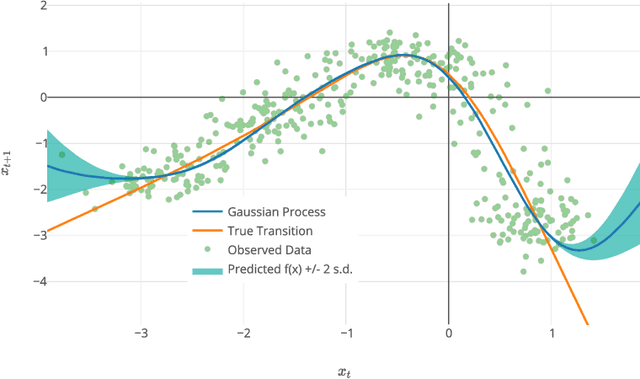
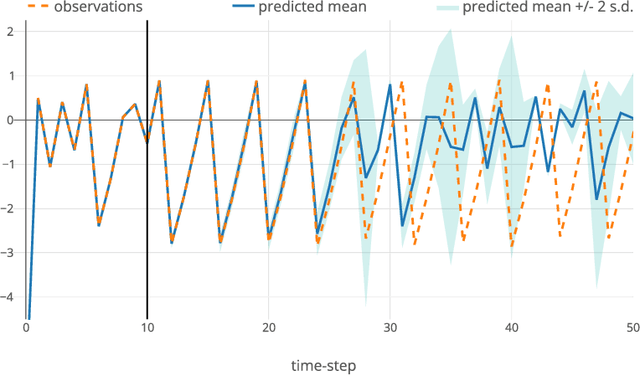
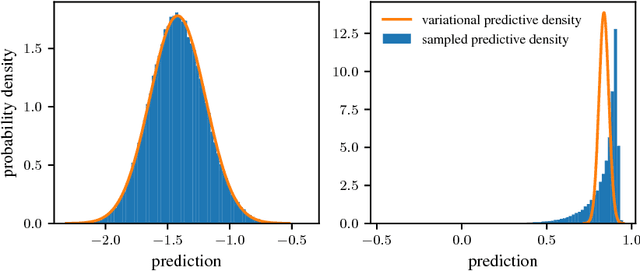
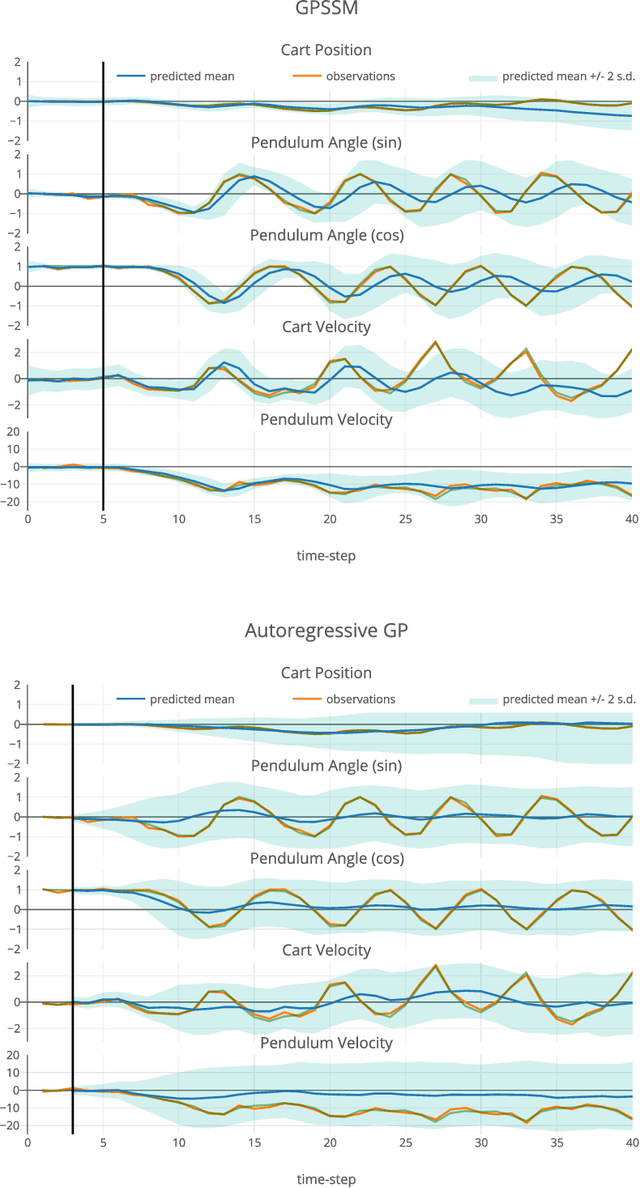
Abstract:We examine an analytic variational inference scheme for the Gaussian Process State Space Model (GPSSM) - a probabilistic model for system identification and time-series modelling. Our approach performs variational inference over both the system states and the transition function. We exploit Markov structure in the true posterior, as well as an inducing point approximation to achieve linear time complexity in the length of the time series. Contrary to previous approaches, no Monte Carlo sampling is required: inference is cast as a deterministic optimisation problem. In a number of experiments, we demonstrate the ability to model non-linear dynamics in the presence of both process and observation noise as well as to impute missing information (e.g. velocities from raw positions through time), to de-noise, and to estimate the underlying dimensionality of the system. Finally, we also introduce a closed-form method for multi-step prediction, and a novel criterion for assessing the quality of our approximate posterior.
Quantum machine learning: a classical perspective
Feb 13, 2018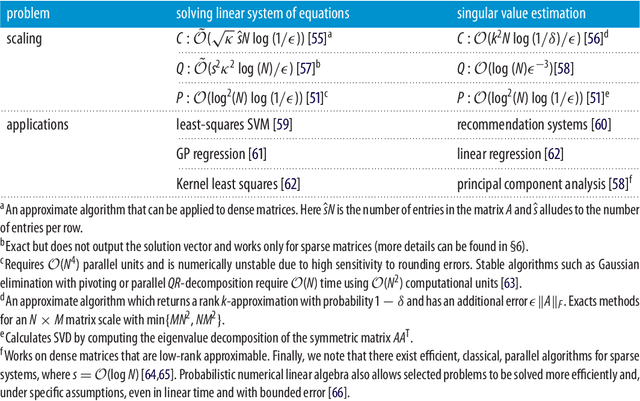
Abstract:Recently, increased computational power and data availability, as well as algorithmic advances, have led machine learning techniques to impressive results in regression, classification, data-generation and reinforcement learning tasks. Despite these successes, the proximity to the physical limits of chip fabrication alongside the increasing size of datasets are motivating a growing number of researchers to explore the possibility of harnessing the power of quantum computation to speed-up classical machine learning algorithms. Here we review the literature in quantum machine learning and discuss perspectives for a mixed readership of classical machine learning and quantum computation experts. Particular emphasis will be placed on clarifying the limitations of quantum algorithms, how they compare with their best classical counterparts and why quantum resources are expected to provide advantages for learning problems. Learning in the presence of noise and certain computationally hard problems in machine learning are identified as promising directions for the field. Practical questions, like how to upload classical data into quantum form, will also be addressed.
* v3 33 pages; typos corrected and references added
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge