Non-Factorised Variational Inference in Dynamical Systems
Paper and Code
Dec 14, 2018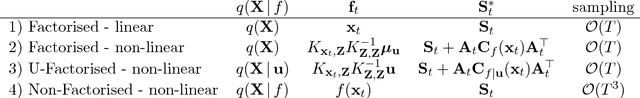
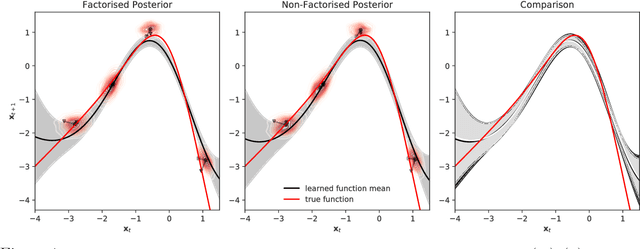
We focus on variational inference in dynamical systems where the discrete time transition function (or evolution rule) is modelled by a Gaussian process. The dominant approach so far has been to use a factorised posterior distribution, decoupling the transition function from the system states. This is not exact in general and can lead to an overconfident posterior over the transition function as well as an overestimation of the intrinsic stochasticity of the system (process noise). We propose a new method that addresses these issues and incurs no additional computational costs.
* 6 pages, 1 figure, 1 table
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge