Approximate Inference for Fully Bayesian Gaussian Process Regression
Paper and Code
Dec 31, 2019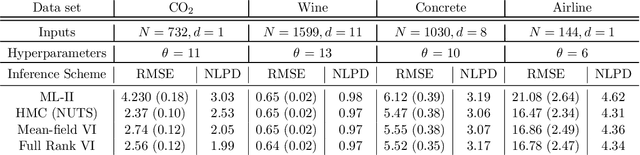
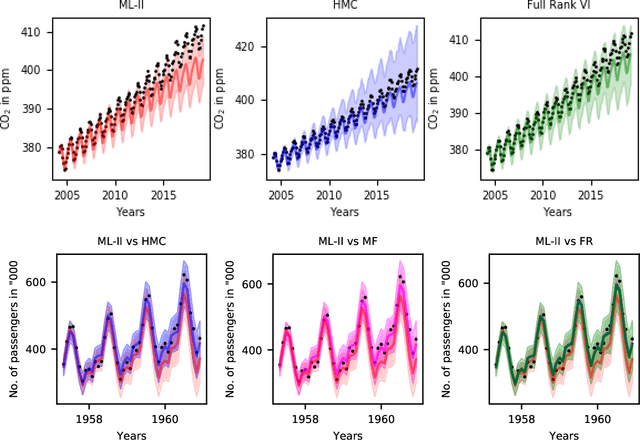

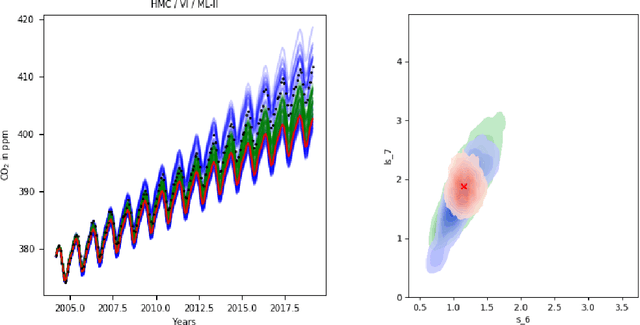
Learning in Gaussian Process models occurs through the adaptation of hyperparameters of the mean and the covariance function. The classical approach entails maximizing the marginal likelihood yielding fixed point estimates (an approach called \textit{Type II maximum likelihood} or ML-II). An alternative learning procedure is to infer the posterior over hyperparameters in a hierarchical specification of GPs we call \textit{Fully Bayesian Gaussian Process Regression} (GPR). This work considers two approximation schemes for the intractable hyperparameter posterior: 1) Hamiltonian Monte Carlo (HMC) yielding a sampling-based approximation and 2) Variational Inference (VI) where the posterior over hyperparameters is approximated by a factorized Gaussian (mean-field) or a full-rank Gaussian accounting for correlations between hyperparameters. We analyze the predictive performance for fully Bayesian GPR on a range of benchmark data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge