Sparse Gaussian Processes with Spherical Harmonic Features Revisited

We revisit the Gaussian process model with spherical harmonic features and study connections between the associated RKHS, its eigenstructure and deep models. Based on this, we introduce a new class of kernels which correspond to deep models of continuous depth. In our formulation, depth can be estimated as a kernel hyper-parameter by optimizing the evidence lower bound. Further, we introduce sparseness in the eigenbasis by variational learning of the spherical harmonic phases. This enables scaling to larger input dimensions than previously, while also allowing for learning of high frequency variations. We validate our approach on machine learning benchmark datasets.

Double Deep Q Networks for Sensor Management in Space Situational Awareness

We present a novel Double Deep Q Network (DDQN) application to a sensor management problem in space situational awareness (SSA). Frequent launches of satellites into Earth orbit pose a significant sensor management challenge, whereby a limited number of sensors are required to detect and track an increasing number of objects. In this paper, we demonstrate the use of reinforcement learning to develop a sensor management policy for SSA. We simulate a controllable Earth-based telescope, which is trained to maximise the number of satellites tracked using an extended Kalman filter. The estimated state covariance matrices for satellites observed under the DDQN policy are greatly reduced compared to those generated by an alternate (random) policy. This work provides the basis for further advancements and motivates the use of reinforcement learning for SSA.

Comparing Classes of Estimators: When does Gradient Descent Beat Ridge Regression in Linear Models?

Modern methods for learning from data depend on many tuning parameters, such as the stepsize for optimization methods, and the regularization strength for regularized learning methods. Since performance can depend strongly on these parameters, it is important to develop comparisons between \emph{classes of methods}, not just for particularly tuned ones. Here, we take aim to compare classes of estimators via the relative performance of the \emph{best method in the class}. This allows us to rigorously quantify the tuning sensitivity of learning algorithms. As an illustration, we investigate the statistical estimation performance of ridge regression with a uniform grid of regularization parameters, and of gradient descent iterates with a fixed stepsize, in the standard linear model with a random isotropic ground truth parameter. (1) For orthogonal designs, we find the \emph{exact minimax optimal classes of estimators}, showing they are equal to gradient descent with a polynomially decaying learning rate. We find the exact suboptimalities of ridge regression and gradient descent with a fixed stepsize, showing that they decay as either $1/k$ or $1/k^2$ for specific ranges of $k$ estimators. (2) For general designs with a large number of non-zero eigenvalues, we find that gradient descent outperforms ridge regression when the eigenvalues decay slowly, as a power law with exponent less than unity. If instead the eigenvalues decay quickly, as a power law with exponent greater than unity or exponentially, we find that ridge regression outperforms gradient descent. Our results highlight the importance of tuning parameters. In particular, while optimally tuned ridge regression is the best estimator in our case, it can be outperformed by gradient descent when both are restricted to being tuned over a finite regularization grid.

Stability & Generalisation of Gradient Descent for Shallow Neural Networks without the Neural Tangent Kernel

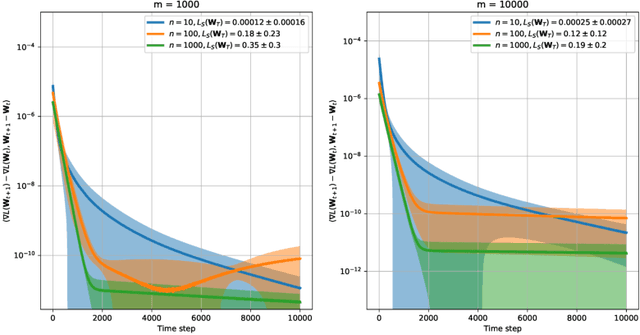
We revisit on-average algorithmic stability of Gradient Descent (GD) for training overparameterised shallow neural networks and prove new generalisation and excess risk bounds without the Neural Tangent Kernel (NTK) or Polyak-{\L}ojasiewicz (PL) assumptions. In particular, we show oracle type bounds which reveal that the generalisation and excess risk of GD is controlled by an interpolating network with the shortest GD path from initialisation (in a sense, an interpolating network with the smallest relative norm). While this was known for kernelised interpolants, our proof applies directly to networks trained by GD without intermediate kernelisation. At the same time, by relaxing oracle inequalities developed here we recover existing NTK-based risk bounds in a straightforward way, which demonstrates that our analysis is tighter. Finally, unlike most of the NTK-based analyses we focus on regression with label noise and show that GD with early stopping is consistent.

Learning with Gradient Descent and Weakly Convex Losses

We study the learning performance of gradient descent when the empirical risk is weakly convex, namely, the smallest negative eigenvalue of the empirical risk's Hessian is bounded in magnitude. By showing that this eigenvalue can control the stability of gradient descent, generalisation error bounds are proven that hold under a wider range of step sizes compared to previous work. Out of sample guarantees are then achieved by decomposing the test error into generalisation, optimisation and approximation errors, each of which can be bounded and traded off with respect to algorithmic parameters, sample size and magnitude of this eigenvalue. In the case of a two layer neural network, we demonstrate that the empirical risk can satisfy a notion of local weak convexity, specifically, the Hessian's smallest eigenvalue during training can be controlled by the normalisation of the layers, i.e., network scaling. This allows test error guarantees to then be achieved when the population risk minimiser satisfies a complexity assumption. By trading off the network complexity and scaling, insights are gained into the implicit bias of neural network scaling, which are further supported by experimental findings.

Decentralised Learning with Random Features and Distributed Gradient Descent

We investigate the generalisation performance of Distributed Gradient Descent with Implicit Regularisation and Random Features in the homogenous setting where a network of agents are given data sampled independently from the same unknown distribution. Along with reducing the memory footprint, Random Features are particularly convenient in this setting as they provide a common parameterisation across agents that allows to overcome previous difficulties in implementing Decentralised Kernel Regression. Under standard source and capacity assumptions, we establish high probability bounds on the predictive performance for each agent as a function of the step size, number of iterations, inverse spectral gap of the communication matrix and number of Random Features. By tuning these parameters, we obtain statistical rates that are minimax optimal with respect to the total number of samples in the network. The algorithm provides a linear improvement over single machine Gradient Descent in memory cost and, when agents hold enough data with respect to the network size and inverse spectral gap, a linear speed-up in computational runtime for any network topology. We present simulations that show how the number of Random Features, iterations and samples impact predictive performance.

Asymptotics of Ridge(less) Regression under General Source Condition

We analyze the prediction performance of ridge and ridgeless regression when both the number and the dimension of the data go to infinity. In particular, we consider a general setting introducing prior assumptions characterizing "easy" and "hard" learning problems. In this setting, we show that ridgeless (zero regularisation) regression is optimal for easy problems with a high signal to noise. Furthermore, we show that additional descents in the ridgeless bias and variance learning curve can occur beyond the interpolating threshold, verifying recent empirical observations. More generally, we show how a variety of learning curves are possible depending on the problem at hand. From a technical point of view, characterising the influence of prior assumptions requires extending previous applications of random matrix theory to study ridge regression.

Decentralised Sparse Multi-Task Regression

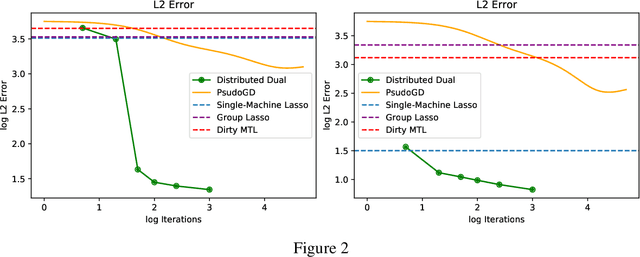
We consider a sparse multi-task regression framework for fitting a collection of related sparse models. Representing models as nodes in a graph with edges between related models, a framework that fuses lasso regressions with the total variation penalty is investigated. Under a form of restricted eigenvalue assumption, bounds on prediction and squared error are given that depend upon the sparsity of each model and the differences between related models. This assumption relates to the smallest eigenvalue restricted to the intersection of two cone sets of the covariance matrix constructed from each of the agents' covariances. We show that this assumption can be satisfied if the constructed covariance matrix satisfies a restricted isometry property. In the case of a grid topology high-probability bounds are given that match, up to log factors, the no-communication setting of fitting a lasso on each model, divided by the number of agents. A decentralised dual method that exploits a convex-concave formulation of the penalised problem is proposed to fit the models and its effectiveness demonstrated on simulations against the group lasso and variants.

Optimal Statistical Rates for Decentralised Non-Parametric Regression with Linear Speed-Up

We analyse the learning performance of Distributed Gradient Descent in the context of multi-agent decentralised non-parametric regression with the square loss function when i.i.d. samples are assigned to agents. We show that if agents hold sufficiently many samples with respect to the network size, then Distributed Gradient Descent achieves optimal statistical rates with a number of iterations that scales, up to a threshold, with the inverse of the spectral gap of the gossip matrix divided by the number of samples owned by each agent raised to a problem-dependent power. The presence of the threshold comes from statistics. It encodes the existence of a "big data" regime where the number of required iterations does not depend on the network topology. In this regime, Distributed Gradient Descent achieves optimal statistical rates with the same order of iterations as gradient descent run with all the samples in the network. Provided the communication delay is sufficiently small, the distributed protocol yields a linear speed-up in runtime compared to the single-machine protocol. This is in contrast to decentralised optimisation algorithms that do not exploit statistics and only yield a linear speed-up in graphs where the spectral gap is bounded away from zero. Our results exploit the statistical concentration of quantities held by agents and shed new light on the interplay between statistics and communication in decentralised methods. Bounds are given in the standard non-parametric setting with source/capacity assumptions.

Graph-Dependent Implicit Regularisation for Distributed Stochastic Subgradient Descent

We propose graph-dependent implicit regularisation strategies for distributed stochastic subgradient descent (Distributed SGD) for convex problems in multi-agent learning. Under the standard assumptions of convexity, Lipschitz continuity, and smoothness, we establish statistical learning rates that retain, up to logarithmic terms, centralised statistical guarantees through implicit regularisation (step size tuning and early stopping) with appropriate dependence on the graph topology. Our approach avoids the need for explicit regularisation in decentralised learning problems, such as adding constraints to the empirical risk minimisation rule. Particularly for distributed methods, the use of implicit regularisation allows the algorithm to remain simple, without projections or dual methods. To prove our results, we establish graph-independent generalisation bounds for Distributed SGD that match the centralised setting (using algorithmic stability), and we establish graph-dependent optimisation bounds that are of independent interest. We present numerical experiments to show that the qualitative nature of the upper bounds we derive can be representative of real behaviours.