Decentralised Sparse Multi-Task Regression

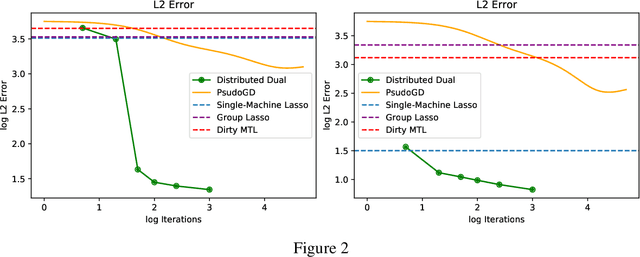
We consider a sparse multi-task regression framework for fitting a collection of related sparse models. Representing models as nodes in a graph with edges between related models, a framework that fuses lasso regressions with the total variation penalty is investigated. Under a form of restricted eigenvalue assumption, bounds on prediction and squared error are given that depend upon the sparsity of each model and the differences between related models. This assumption relates to the smallest eigenvalue restricted to the intersection of two cone sets of the covariance matrix constructed from each of the agents' covariances. We show that this assumption can be satisfied if the constructed covariance matrix satisfies a restricted isometry property. In the case of a grid topology high-probability bounds are given that match, up to log factors, the no-communication setting of fitting a lasso on each model, divided by the number of agents. A decentralised dual method that exploits a convex-concave formulation of the penalised problem is proposed to fit the models and its effectiveness demonstrated on simulations against the group lasso and variants.

Individualized Rank Aggregation using Nuclear Norm Regularization

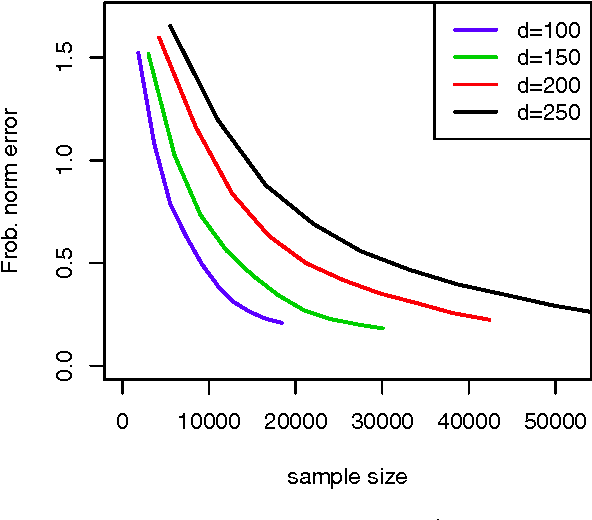
In recent years rank aggregation has received significant attention from the machine learning community. The goal of such a problem is to combine the (partially revealed) preferences over objects of a large population into a single, relatively consistent ordering of those objects. However, in many cases, we might not want a single ranking and instead opt for individual rankings. We study a version of the problem known as collaborative ranking. In this problem we assume that individual users provide us with pairwise preferences (for example purchasing one item over another). From those preferences we wish to obtain rankings on items that the users have not had an opportunity to explore. The results here have a very interesting connection to the standard matrix completion problem. We provide a theoretical justification for a nuclear norm regularized optimization procedure, and provide high-dimensional scaling results that show how the error in estimating user preferences behaves as the number of observations increase.

Fast global convergence of gradient methods for high-dimensional statistical recovery

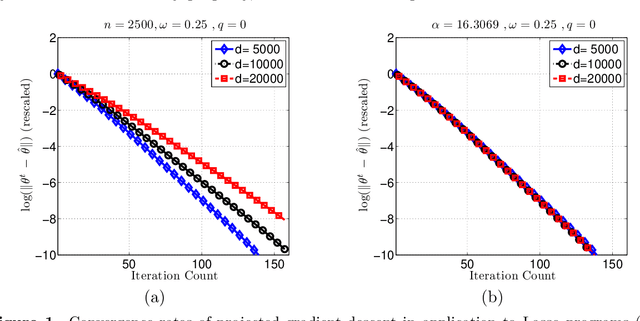
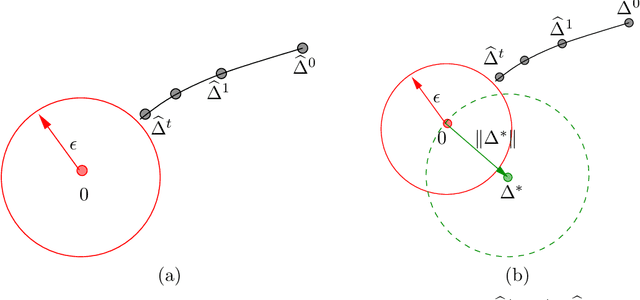
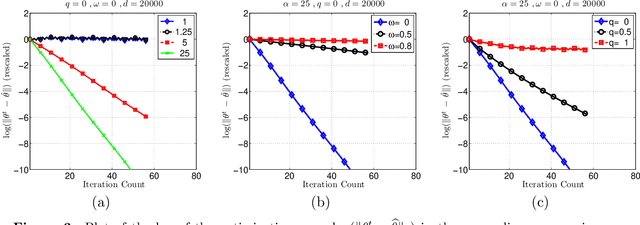
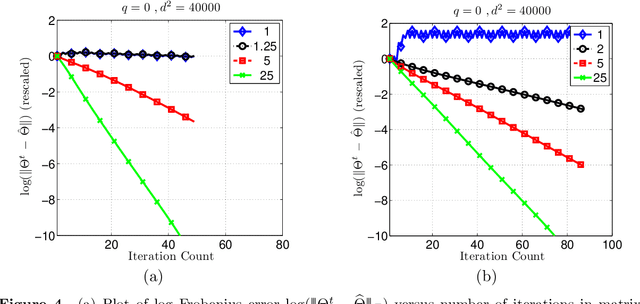
Many statistical $M$-estimators are based on convex optimization problems formed by the combination of a data-dependent loss function with a norm-based regularizer. We analyze the convergence rates of projected gradient and composite gradient methods for solving such problems, working within a high-dimensional framework that allows the data dimension $\pdim$ to grow with (and possibly exceed) the sample size $\numobs$. This high-dimensional structure precludes the usual global assumptions---namely, strong convexity and smoothness conditions---that underlie much of classical optimization analysis. We define appropriately restricted versions of these conditions, and show that they are satisfied with high probability for various statistical models. Under these conditions, our theory guarantees that projected gradient descent has a globally geometric rate of convergence up to the \emph{statistical precision} of the model, meaning the typical distance between the true unknown parameter $\theta^*$ and an optimal solution $\hat{\theta}$. This result is substantially sharper than previous convergence results, which yielded sublinear convergence, or linear convergence only up to the noise level. Our analysis applies to a wide range of $M$-estimators and statistical models, including sparse linear regression using Lasso ($\ell_1$-regularized regression); group Lasso for block sparsity; log-linear models with regularization; low-rank matrix recovery using nuclear norm regularization; and matrix decomposition. Overall, our analysis reveals interesting connections between statistical precision and computational efficiency in high-dimensional estimation.

Noisy matrix decomposition via convex relaxation: Optimal rates in high dimensions

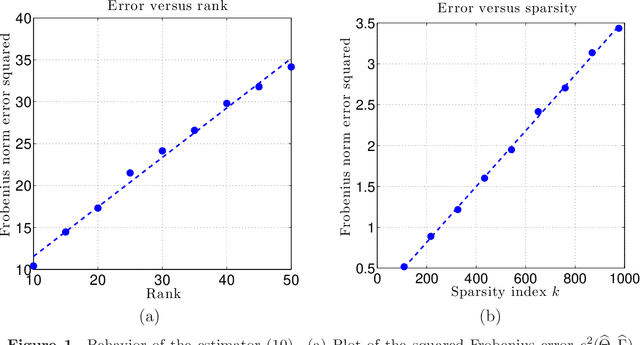
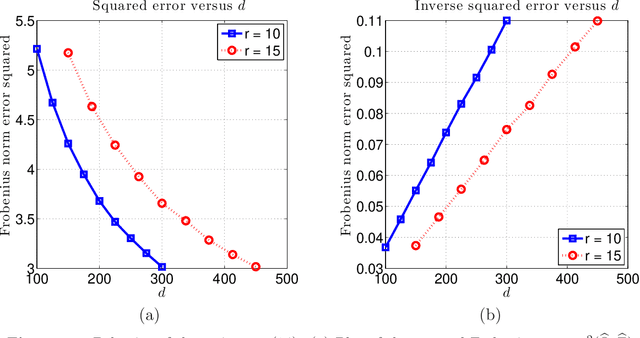
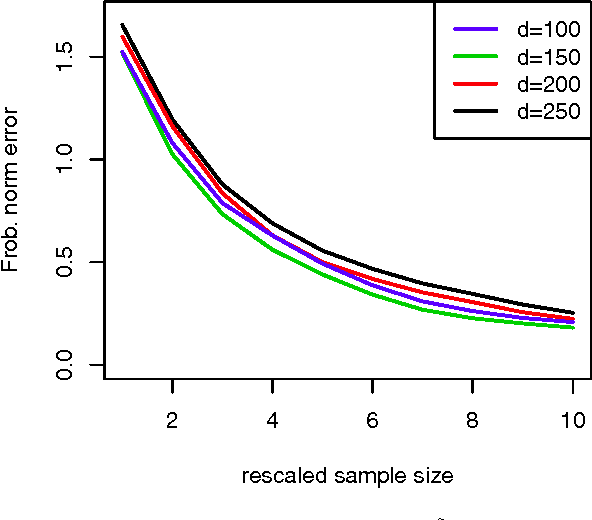
We analyze a class of estimators based on convex relaxation for solving high-dimensional matrix decomposition problems. The observations are noisy realizations of a linear transformation $\mathfrak{X}$ of the sum of an approximately) low rank matrix $\Theta^\star$ with a second matrix $\Gamma^\star$ endowed with a complementary form of low-dimensional structure; this set-up includes many statistical models of interest, including factor analysis, multi-task regression, and robust covariance estimation. We derive a general theorem that bounds the Frobenius norm error for an estimate of the pair $(\Theta^\star, \Gamma^\star)$ obtained by solving a convex optimization problem that combines the nuclear norm with a general decomposable regularizer. Our results utilize a "spikiness" condition that is related to but milder than singular vector incoherence. We specialize our general result to two cases that have been studied in past work: low rank plus an entrywise sparse matrix, and low rank plus a columnwise sparse matrix. For both models, our theory yields non-asymptotic Frobenius error bounds for both deterministic and stochastic noise matrices, and applies to matrices $\Theta^\star$ that can be exactly or approximately low rank, and matrices $\Gamma^\star$ that can be exactly or approximately sparse. Moreover, for the case of stochastic noise matrices and the identity observation operator, we establish matching lower bounds on the minimax error. The sharpness of our predictions is confirmed by numerical simulations.