Individualized Rank Aggregation using Nuclear Norm Regularization
Paper and Code
Oct 03, 2014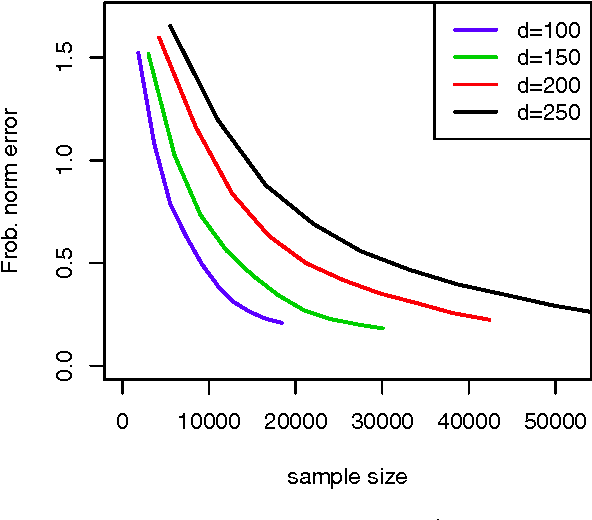
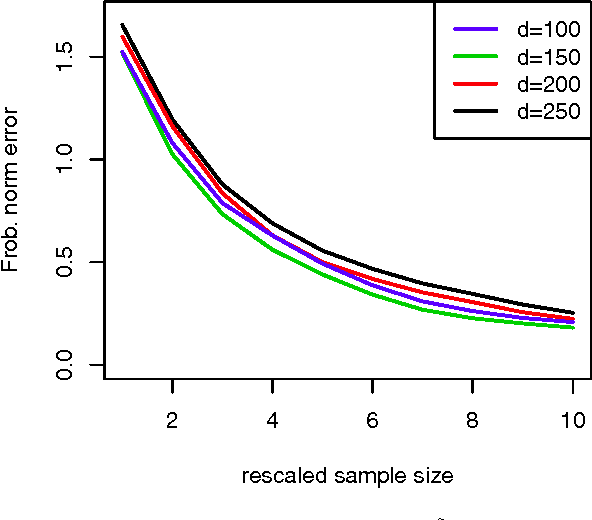
In recent years rank aggregation has received significant attention from the machine learning community. The goal of such a problem is to combine the (partially revealed) preferences over objects of a large population into a single, relatively consistent ordering of those objects. However, in many cases, we might not want a single ranking and instead opt for individual rankings. We study a version of the problem known as collaborative ranking. In this problem we assume that individual users provide us with pairwise preferences (for example purchasing one item over another). From those preferences we wish to obtain rankings on items that the users have not had an opportunity to explore. The results here have a very interesting connection to the standard matrix completion problem. We provide a theoretical justification for a nuclear norm regularized optimization procedure, and provide high-dimensional scaling results that show how the error in estimating user preferences behaves as the number of observations increase.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge