Self Interference Management in In-Band Full-Duplex Systems

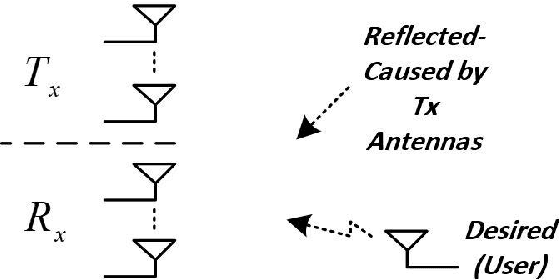
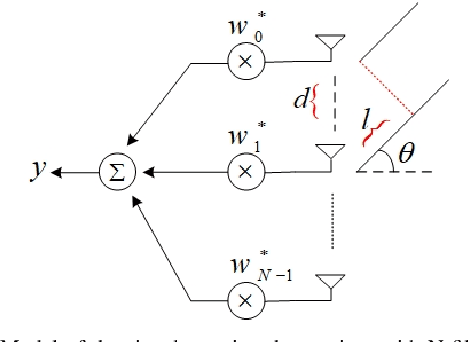
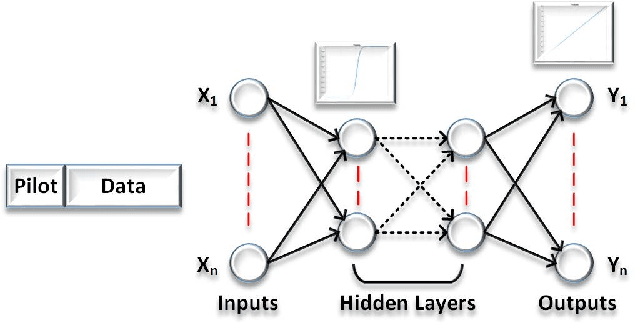
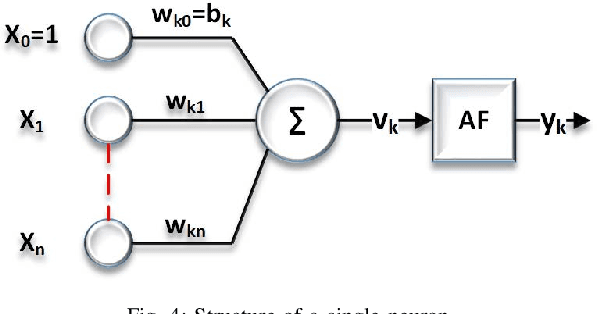
The evolution of wireless systems has led to a continuous increase in the demand for radio frequency spectrum. To address this issue, a technology that has received a lot of attention is In-Band Full-Duplex (IBFD). The interest in IBFD systems stems from its capability to simultaneously transmit and receive data in the same frequency. Cancelling the self interference (SI) from the transmitter to the collocated receiver plays a pivotal role in the performance of the system. There are two types of SI cancellation (SIC) approaches, passive and active. In this research, the focus is on active cancellation and, in particular, SIC in the digital domain. Among the direct and backscattered SI, the former has been studied for a long time; therefore, the backscatter is considered in this research and two SIC approaches are analyzed. The first achieves SIC through beamforming. This requires knowing the angle of the received SI to put the beam null-space in this direction. The second method removes SI by employing an Artificial Neural Networks (ANNs). Using an ANN, there is no need to know the direction of the SI. The neural network is trained with pilots which results in the network being able to separate the desired signal from the SI at the receiver. Bayesian Neural Networks show the importance of the weights and assign a parameter that facilitates ignoring the less significant ones. Through comparative simulations we demonstrate that the ANN-based SIC achieves equivalent bit error rate performance as two beamforming methods.

AI-Driven Demodulators for Nonlinear Receivers in Shared Spectrum with High-Power Blockers

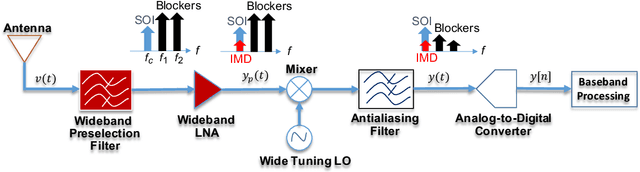
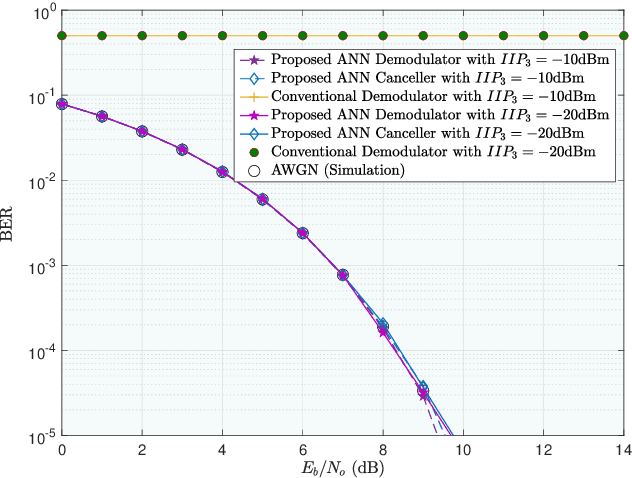
Research has shown that communications systems and receivers suffer from high power adjacent channel signals, called blockers, that drive the radio frequency (RF) front end into nonlinear operation. Since simple systems, such as the Internet of Things (IoT), will coexist with sophisticated communications transceivers, radars and other spectrum consumers, these need to be protected employing a simple, yet adaptive solution to RF nonlinearity. This paper therefore proposes a flexible data driven approach that uses a simple artificial neural network (ANN) to aid in the removal of the third order intermodulation distortion (IMD) as part of the demodulation process. We introduce and numerically evaluate two artificial intelligence (AI)-enhanced receivers-ANN as the IMD canceler and ANN as the demodulator. Our results show that a simple ANN structure can significantly improve the bit error rate (BER) performance of nonlinear receivers with strong blockers and that the ANN architecture and configuration depends mainly on the RF front end characteristics, such as the third order intercept point (IP3). We therefore recommend that receivers have hardware tags and ways to monitor those over time so that the AI and software radio processing stack can be effectively customized and automatically updated to deal with changing operating conditions.

Emulating dynamic non-linear simulators using Gaussian processes

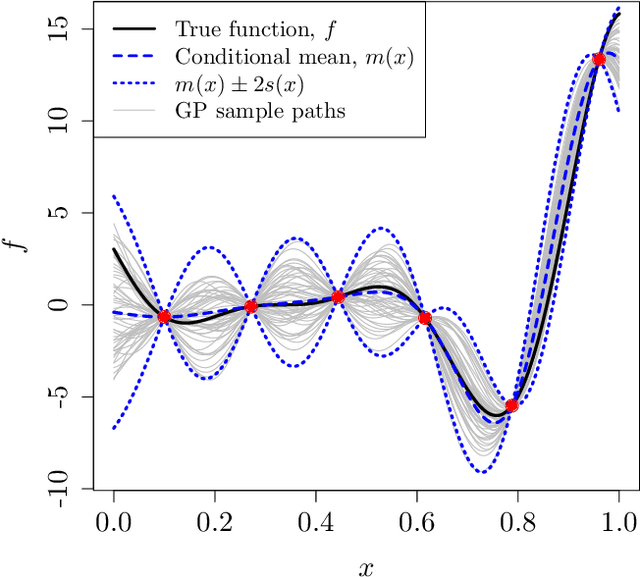
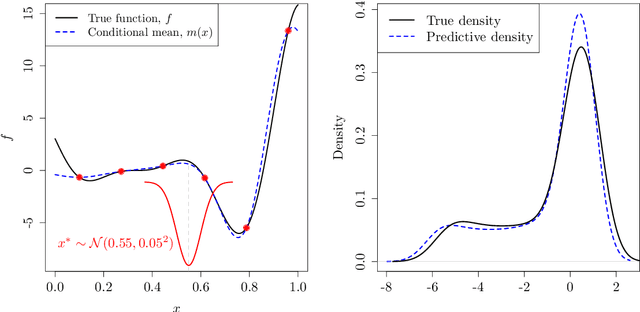
In this paper, we examine the emulation of non-linear deterministic computer codes where the output is a time series, possibly multivariate. Such computer models simulate the evolution of some real-world phenomena over time, for example models of the climate or the functioning of the human brain. The models we are interested in are highly non-linear and exhibit tipping points, bifurcations and chaotic behaviour. However, each simulation run could be too time-consuming to perform analyses that require many runs, including quantifying the variation in model output with respect to changes in the inputs. We therefore build emulators using Gaussian processes to approximate the output of the code. We use the Gaussian process to predict one-step ahead in an iterative way over the whole time series. We consider a number of ways to propagate uncertainty through the time series including both the uncertainty of inputs to the emulators at time $t$ and the correlation between them. The methodology is illustrated with a number of examples. These include the highly non-linear dynamical systems described by the Lorenz and Van der Pol equations. In both cases we will show that we not only have very good predictive performance but also have measures of uncertainty that reflect what is known about predictability in each system.

An analytic comparison of regularization methods for Gaussian Processes

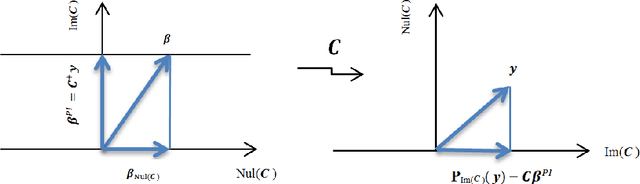
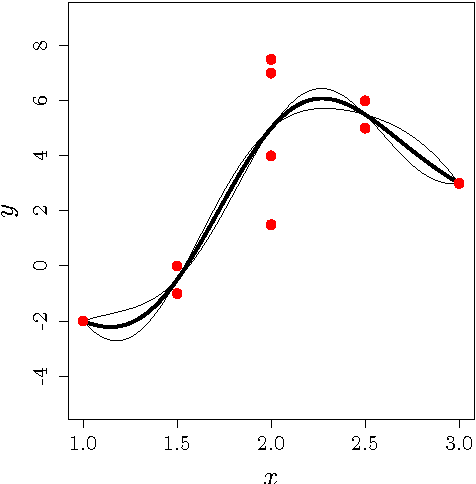
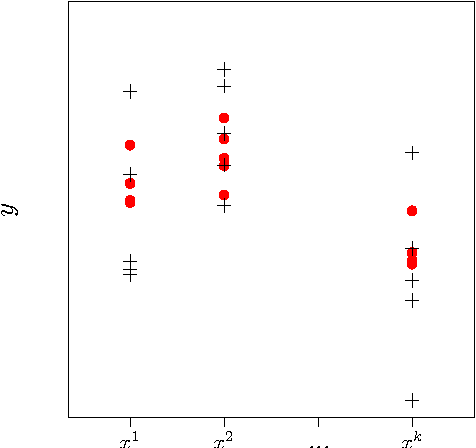
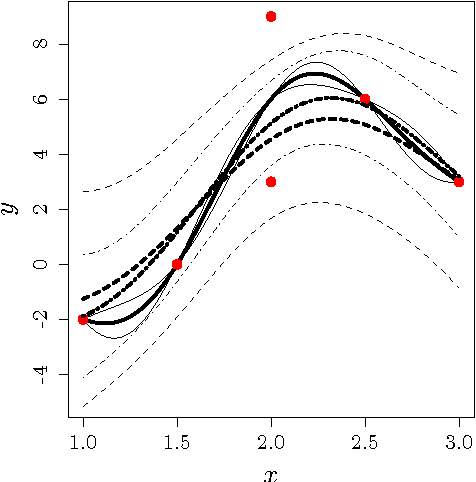
Gaussian Processes (GPs) are a popular approach to predict the output of a parameterized experiment. They have many applications in the field of Computer Experiments, in particular to perform sensitivity analysis, adaptive design of experiments and global optimization. Nearly all of the applications of GPs require the inversion of a covariance matrix that, in practice, is often ill-conditioned. Regularization methodologies are then employed with consequences on the GPs that need to be better understood.The two principal methods to deal with ill-conditioned covariance matrices are i) pseudoinverse and ii) adding a positive constant to the diagonal (the so-called nugget regularization).The first part of this paper provides an algebraic comparison of PI and nugget regularizations. Redundant points, responsible for covariance matrix singularity, are defined. It is proven that pseudoinverse regularization, contrarily to nugget regularization, averages the output values and makes the variance zero at redundant points. However, pseudoinverse and nugget regularizations become equivalent as the nugget value vanishes. A measure for data-model discrepancy is proposed which serves for choosing a regularization technique.In the second part of the paper, a distribution-wise GP is introduced that interpolates Gaussian distributions instead of data points. Distribution-wise GP can be seen as an improved regularization method for GPs.

Small ensembles of kriging models for optimization

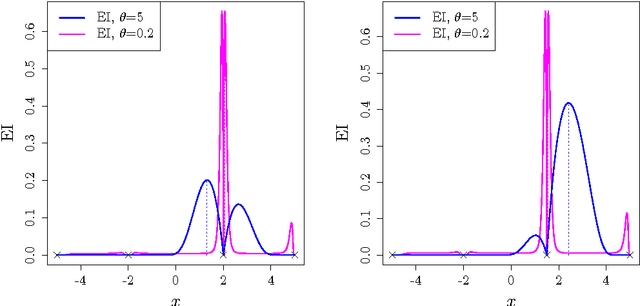
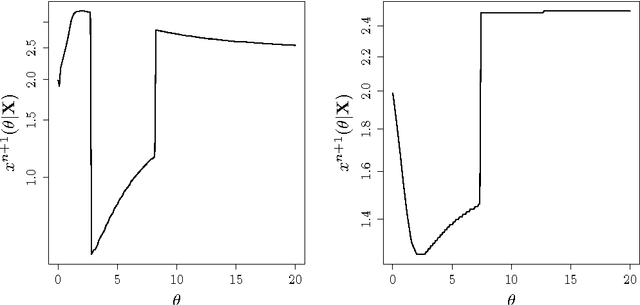
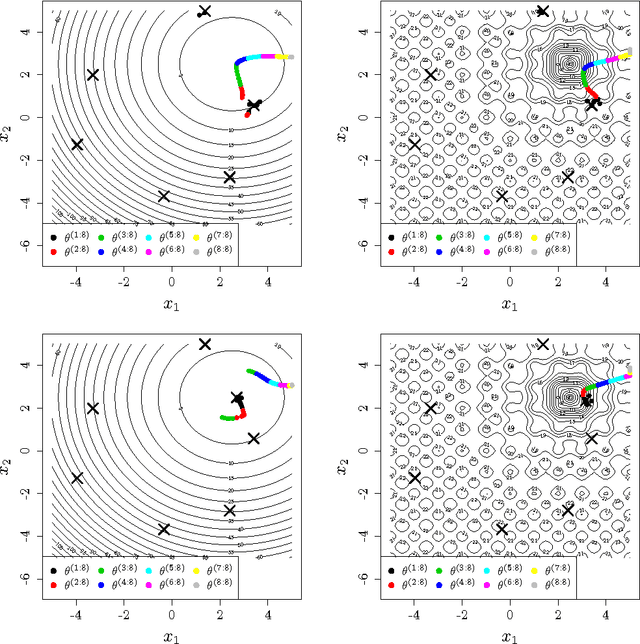
The Efficient Global Optimization (EGO) algorithm uses a conditional Gaus-sian Process (GP) to approximate an objective function known at a finite number of observation points and sequentially adds new points which maximize the Expected Improvement criterion according to the GP. The important factor that controls the efficiency of EGO is the GP covariance function (or kernel) which should be chosen according to the objective function. Traditionally, a pa-rameterized family of covariance functions is considered whose parameters are learned through statistical procedures such as maximum likelihood or cross-validation. However, it may be questioned whether statistical procedures for learning covariance functions are the most efficient for optimization as they target a global agreement between the GP and the observations which is not the ultimate goal of optimization. Furthermore, statistical learning procedures are computationally expensive. The main alternative to the statistical learning of the GP is self-adaptation, where the algorithm tunes the kernel parameters based on their contribution to objective function improvement. After questioning the possibility of self-adaptation for kriging based optimizers, this paper proposes a novel approach for tuning the length-scale of the GP in EGO: At each iteration, a small ensemble of kriging models structured by their length-scales is created. All of the models contribute to an iterate in an EGO-like fashion. Then, the set of models is densified around the model whose length-scale yielded the best iterate and further points are produced. Numerical experiments are provided which motivate the use of many length-scales. The tested implementation does not perform better than the classical EGO algorithm in a sequential context but show the potential of the approach for parallel implementations.