Emulating dynamic non-linear simulators using Gaussian processes
Paper and Code
Jun 09, 2018
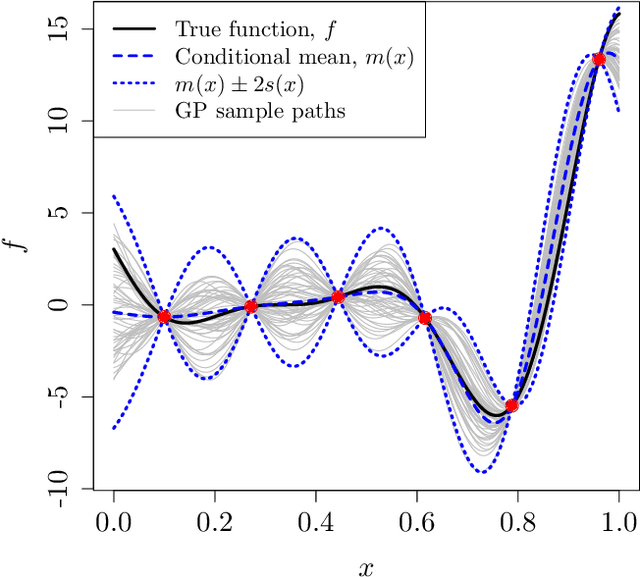
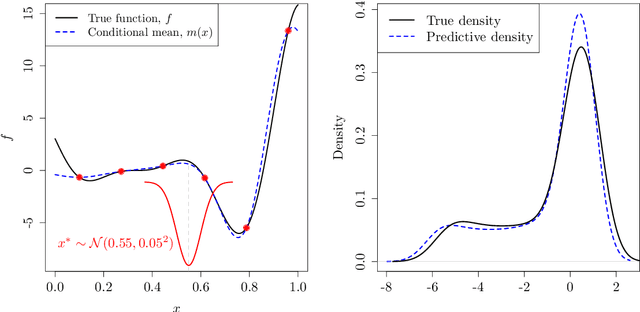

In this paper, we examine the emulation of non-linear deterministic computer codes where the output is a time series, possibly multivariate. Such computer models simulate the evolution of some real-world phenomena over time, for example models of the climate or the functioning of the human brain. The models we are interested in are highly non-linear and exhibit tipping points, bifurcations and chaotic behaviour. However, each simulation run could be too time-consuming to perform analyses that require many runs, including quantifying the variation in model output with respect to changes in the inputs. We therefore build emulators using Gaussian processes to approximate the output of the code. We use the Gaussian process to predict one-step ahead in an iterative way over the whole time series. We consider a number of ways to propagate uncertainty through the time series including both the uncertainty of inputs to the emulators at time $t$ and the correlation between them. The methodology is illustrated with a number of examples. These include the highly non-linear dynamical systems described by the Lorenz and Van der Pol equations. In both cases we will show that we not only have very good predictive performance but also have measures of uncertainty that reflect what is known about predictability in each system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge