An analytic comparison of regularization methods for Gaussian Processes

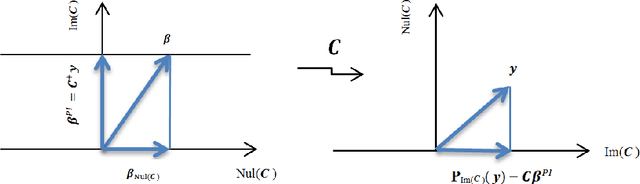
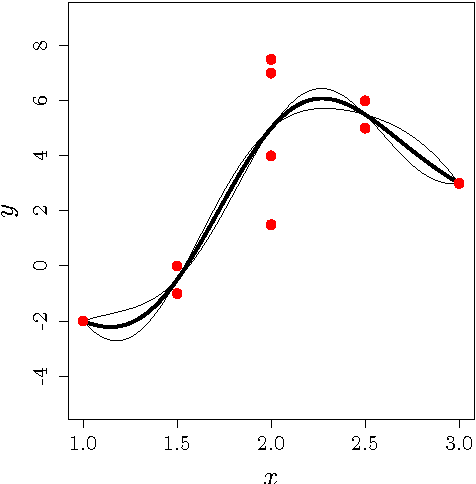
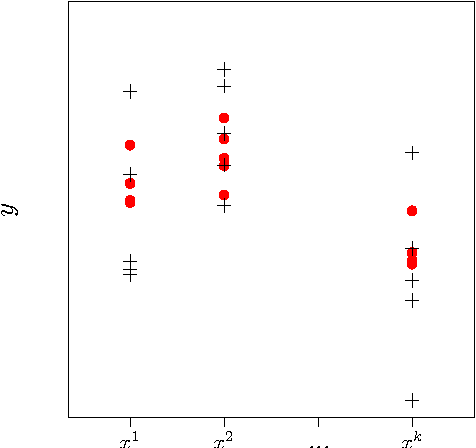
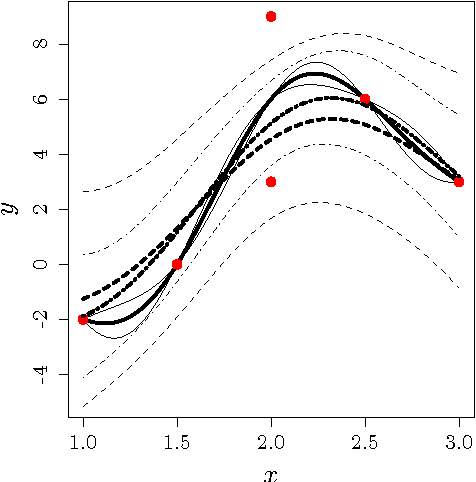
Gaussian Processes (GPs) are a popular approach to predict the output of a parameterized experiment. They have many applications in the field of Computer Experiments, in particular to perform sensitivity analysis, adaptive design of experiments and global optimization. Nearly all of the applications of GPs require the inversion of a covariance matrix that, in practice, is often ill-conditioned. Regularization methodologies are then employed with consequences on the GPs that need to be better understood.The two principal methods to deal with ill-conditioned covariance matrices are i) pseudoinverse and ii) adding a positive constant to the diagonal (the so-called nugget regularization).The first part of this paper provides an algebraic comparison of PI and nugget regularizations. Redundant points, responsible for covariance matrix singularity, are defined. It is proven that pseudoinverse regularization, contrarily to nugget regularization, averages the output values and makes the variance zero at redundant points. However, pseudoinverse and nugget regularizations become equivalent as the nugget value vanishes. A measure for data-model discrepancy is proposed which serves for choosing a regularization technique.In the second part of the paper, a distribution-wise GP is introduced that interpolates Gaussian distributions instead of data points. Distribution-wise GP can be seen as an improved regularization method for GPs.

Small ensembles of kriging models for optimization

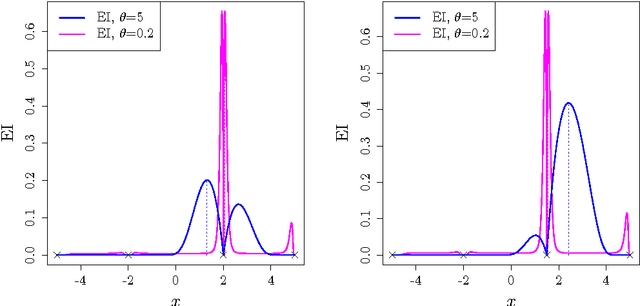
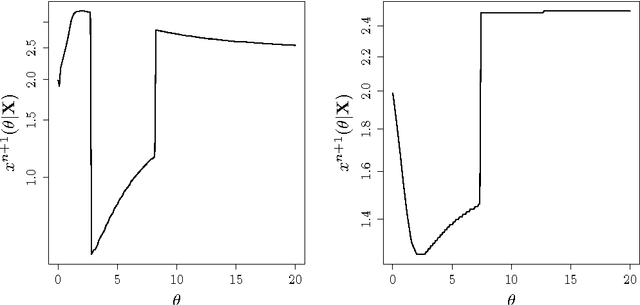
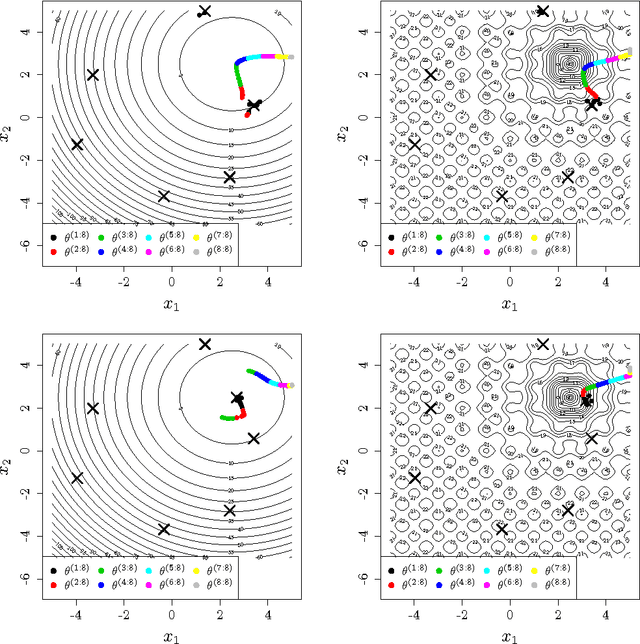
The Efficient Global Optimization (EGO) algorithm uses a conditional Gaus-sian Process (GP) to approximate an objective function known at a finite number of observation points and sequentially adds new points which maximize the Expected Improvement criterion according to the GP. The important factor that controls the efficiency of EGO is the GP covariance function (or kernel) which should be chosen according to the objective function. Traditionally, a pa-rameterized family of covariance functions is considered whose parameters are learned through statistical procedures such as maximum likelihood or cross-validation. However, it may be questioned whether statistical procedures for learning covariance functions are the most efficient for optimization as they target a global agreement between the GP and the observations which is not the ultimate goal of optimization. Furthermore, statistical learning procedures are computationally expensive. The main alternative to the statistical learning of the GP is self-adaptation, where the algorithm tunes the kernel parameters based on their contribution to objective function improvement. After questioning the possibility of self-adaptation for kriging based optimizers, this paper proposes a novel approach for tuning the length-scale of the GP in EGO: At each iteration, a small ensemble of kriging models structured by their length-scales is created. All of the models contribute to an iterate in an EGO-like fashion. Then, the set of models is densified around the model whose length-scale yielded the best iterate and further points are produced. Numerical experiments are provided which motivate the use of many length-scales. The tested implementation does not perform better than the classical EGO algorithm in a sequential context but show the potential of the approach for parallel implementations.