Gradient-based Active Learning with Gaussian Processes for Global Sensitivity Analysis

Global sensitivity analysis of complex numerical simulators is often limited by the small number of model evaluations that can be afforded. In such settings, surrogate models built from a limited set of simulations can substantially reduce the computational burden, provided that the design of computer experiments is enriched efficiently. In this context, we propose an active learning approach that, for a fixed evaluation budget, targets the most informative regions of the input space to improve sensitivity analysis accuracy. More specifically, our method builds on recent advances in active learning for sensitivity analysis (Sobol' indices and derivative-based global sensitivity measures, DGSM) that exploit derivatives obtained from a Gaussian process (GP) surrogate. By leveraging the joint posterior distribution of the GP gradient, we develop acquisition functions that better account for correlations between partial derivatives and their impact on the response surface, leading to a more comprehensive and robust methodology than existing DGSM-oriented criteria. The proposed approach is first compared to state-of-the-art methods on standard benchmark functions, and is then applied to a real environmental model of pesticide transfers.

A sampling criterion for constrained Bayesian optimization with uncertainties

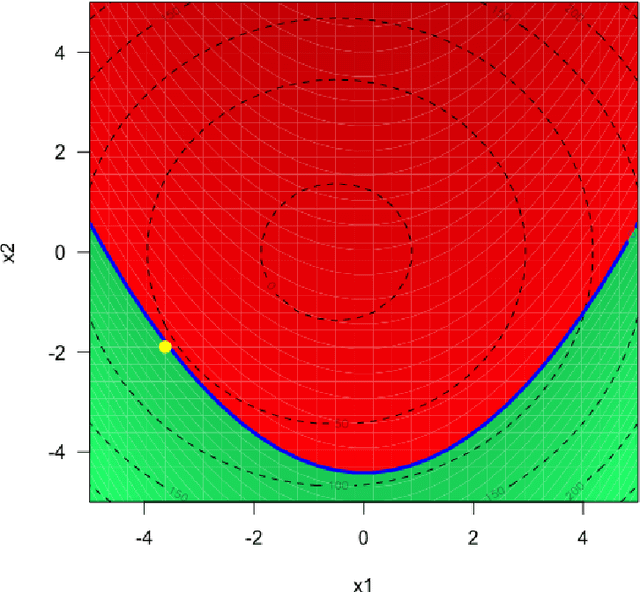
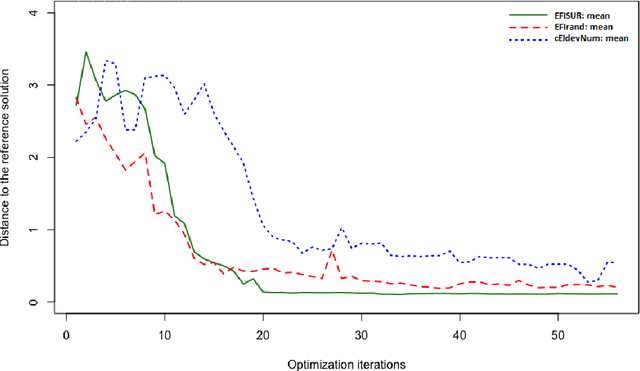
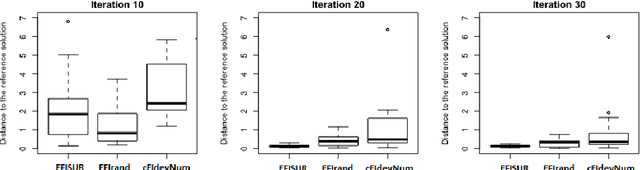
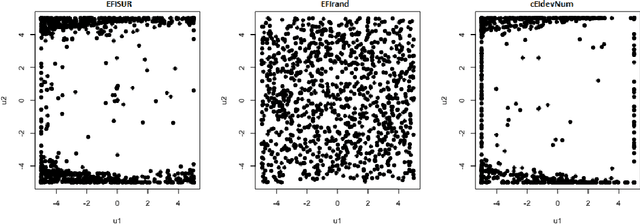
We consider the problem of chance constrained optimization where it is sought to optimize a function and satisfy constraints, both of which are affected by uncertainties. The real world declinations of this problem are particularly challenging because of their inherent computational cost. To tackle such problems, we propose a new Bayesian optimization method. It applies to the situation where the uncertainty comes from some of the inputs, so that it becomes possible to define an acquisition criterion in the joint controlled-uncontrolled input space. The main contribution of this work is an acquisition criterion that accounts for both the average improvement in objective function and the constraint reliability. The criterion is derived following the Stepwise Uncertainty Reduction logic and its maximization provides both optimal controlled and uncontrolled parameters. Analytical expressions are given to efficiently calculate the criterion. Numerical studies on test functions are presented. It is found through experimental comparisons with alternative sampling criteria that the adequation between the sampling criterion and the problem contributes to the efficiency of the overall optimization. As a side result, an expression for the variance of the improvement is given.