A general error analysis for randomized low-rank approximation with application to data assimilation

Randomized algorithms have proven to perform well on a large class of numerical linear algebra problems. Their theoretical analysis is critical to provide guarantees on their behaviour, and in this sense, the stochastic analysis of the randomized low-rank approximation error plays a central role. Indeed, several randomized methods for the approximation of dominant eigen- or singular modes can be rewritten as low-rank approximation methods. However, despite the large variety of algorithms, the existing theoretical frameworks for their analysis rely on a specific structure for the covariance matrix that is not adapted to all the algorithms. We propose a general framework for the stochastic analysis of the low-rank approximation error in Frobenius norm for centered and non-standard Gaussian matrices. Under minimal assumptions on the covariance matrix, we derive accurate bounds both in expectation and probability. Our bounds have clear interpretations that enable us to derive properties and motivate practical choices for the covariance matrix resulting in efficient low-rank approximation algorithms. The most commonly used bounds in the literature have been demonstrated as a specific instance of the bounds proposed here, with the additional contribution of being tighter. Numerical experiments related to data assimilation further illustrate that exploiting the problem structure to select the covariance matrix improves the performance as suggested by our bounds.

On the approximation of the solution of partial differential equations by artificial neural networks trained by a multilevel Levenberg-Marquardt method

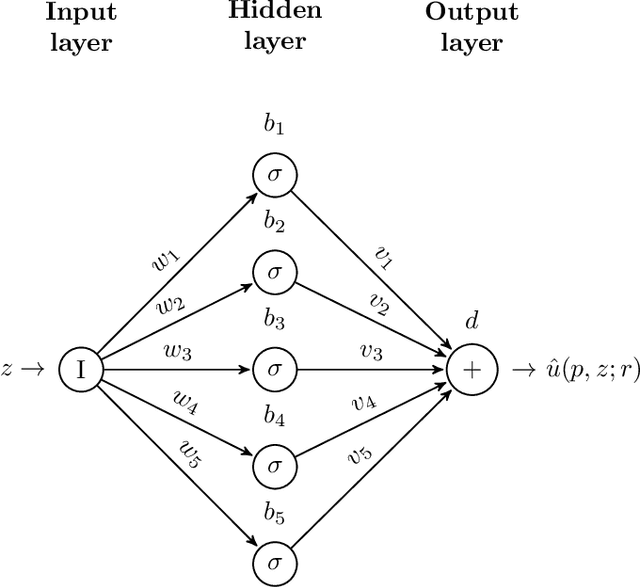
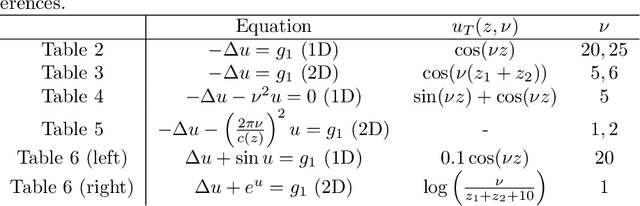
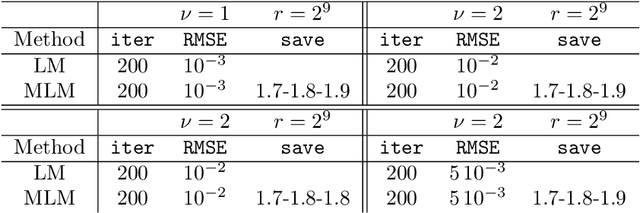
This paper is concerned with the approximation of the solution of partial differential equations by means of artificial neural networks. Here a feedforward neural network is used to approximate the solution of the partial differential equation. The learning problem is formulated as a least squares problem, choosing the residual of the partial differential equation as a loss function, whereas a multilevel Levenberg-Marquardt method is employed as a training method. This setting allows us to get further insight into the potential of multilevel methods. Indeed, when the least squares problem arises from the training of artificial neural networks, the variables subject to optimization are not related by any geometrical constraints and the standard interpolation and restriction operators cannot be employed any longer. A heuristic, inspired by algebraic multigrid methods, is then proposed to construct the multilevel transfer operators. Numerical experiments show encouraging results related to the efficiency of the new multilevel optimization method for the training of artificial neural networks, compared to the standard corresponding one-level procedure.