Charles Audet
A graph-structured distance for heterogeneous datasets with meta variables
May 20, 2024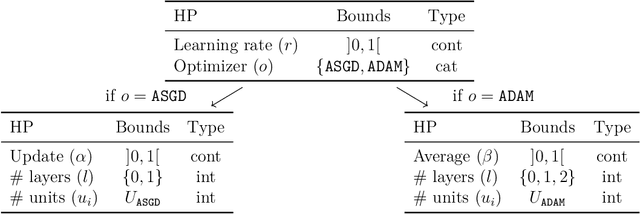
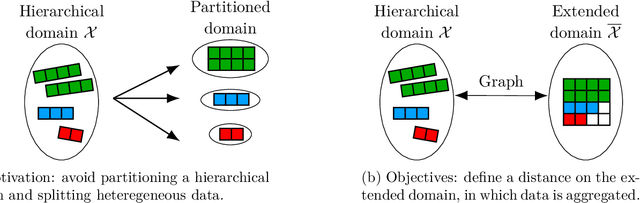

Abstract:Heterogeneous datasets emerge in various machine learning or optimization applications that feature different data sources, various data types and complex relationships between variables. In practice, heterogeneous datasets are often partitioned into smaller well-behaved ones that are easier to process. However, some applications involve expensive-to-generate or limited size datasets, which motivates methods based on the whole dataset. The first main contribution of this work is a modeling graph-structured framework that generalizes state-of-the-art hierarchical, tree-structured, or variable-size frameworks. This framework models domains that involve heterogeneous datasets in which variables may be continuous, integer, or categorical, with some identified as meta if their values determine the inclusion/exclusion or affect the bounds of other so-called decreed variables. Excluded variables are introduced to manage variables that are either included or excluded depending on the given points. The second main contribution is the graph-structured distance that compares extended points with any combination of included and excluded variables: any pair of points can be compared, allowing to work directly in heterogeneous datasets with meta variables. The contributions are illustrated with some regression experiments, in which the performance of a multilayer perceptron with respect to its hyperparameters is modeled with inverse distance weighting and $K$-nearest neighbors models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge