Local Strong Convexity of Source Localization and Error Bound for Target Tracking under Time-of-Arrival Measurements
Paper and Code
Dec 21, 2021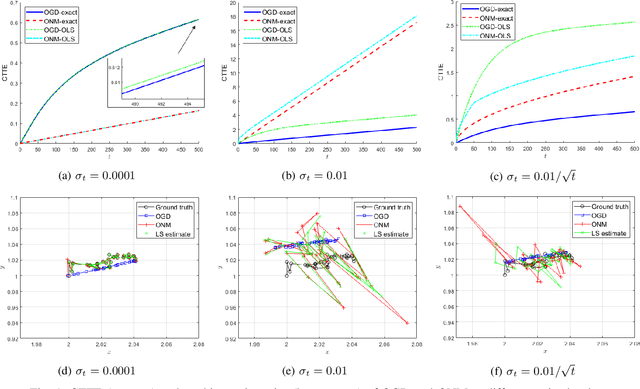
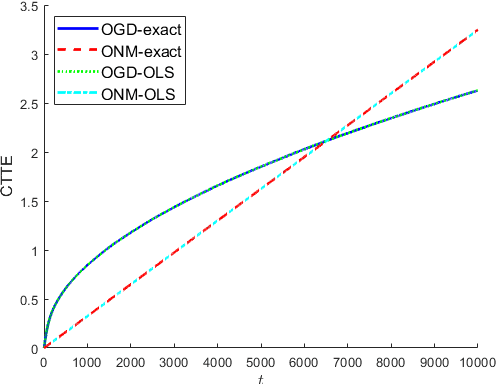
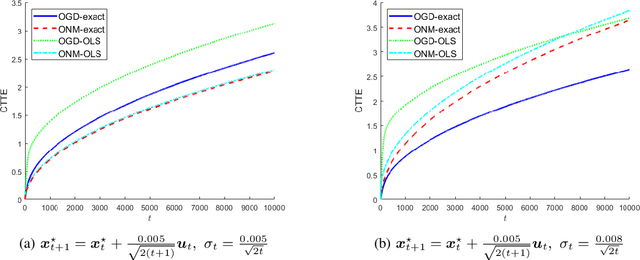
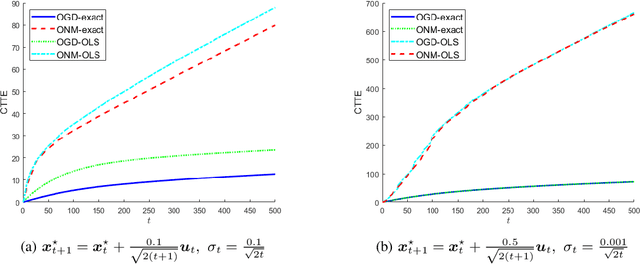
In this paper, we consider a time-varying optimization approach to the problem of tracking a moving target using noisy time-of-arrival (TOA) measurements. Specifically, we formulate the problem as that of sequential TOA-based source localization and apply online gradient descent (OGD) to it to generate the position estimates of the target. To analyze the tracking performance of OGD, we first revisit the classic least-squares formulation of the (static) TOA-based source localization problem and elucidate its estimation and geometric properties. In particular, under standard assumptions on the TOA measurement model, we establish a bound on the distance between an optimal solution to the least-squares formulation and the true target position. Using this bound, we show that the loss function in the formulation, albeit non-convex in general, is locally strongly convex at its global minima. To the best of our knowledge, these results are new and can be of independent interest. By combining them with existing techniques from online strongly convex optimization, we then establish the first non-trivial bound on the cumulative target tracking error of OGD. Our numerical results corroborate the theoretical findings and show that OGD can effectively track the target at different noise levels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge