Multi-agent assignment via state augmented reinforcement learning

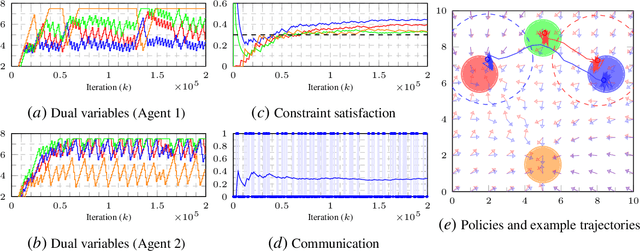
We address the conflicting requirements of a multi-agent assignment problem through constrained reinforcement learning, emphasizing the inadequacy of standard regularization techniques for this purpose. Instead, we recur to a state augmentation approach in which the oscillation of dual variables is exploited by agents to alternate between tasks. In addition, we coordinate the actions of the multiple agents acting on their local states through these multipliers, which are gossiped through a communication network, eliminating the need to access other agent states. By these means, we propose a distributed multi-agent assignment protocol with theoretical feasibility guarantees that we corroborate in a monitoring numerical experiment.

A Networked Multi-Agent System for Mobile Wireless Infrastructure on Demand

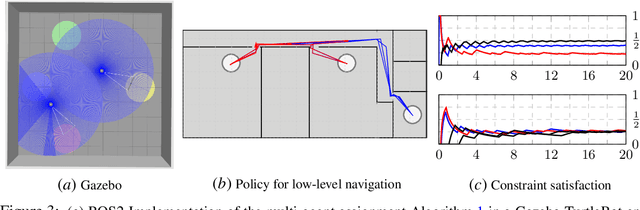
Despite the prevalence of wireless connectivity in urban areas around the globe, there remain numerous and diverse situations where connectivity is insufficient or unavailable. To address this, we introduce mobile wireless infrastructure on demand, a system of UAVs that can be rapidly deployed to establish an ad-hoc wireless network. This network has the capability of reconfiguring itself dynamically to satisfy and maintain the required quality of communication. The system optimizes the positions of the UAVs and the routing of data flows throughout the network to achieve this quality of service (QoS). By these means, task agents using the network simply request a desired QoS, and the system adapts accordingly while allowing them to move freely. We have validated this system both in simulation and in real-world experiments. The results demonstrate that our system effectively offers mobile wireless infrastructure on demand, extending the operational range of task agents and supporting complex mobility patterns, all while ensuring connectivity and being resilient to agent failures.

Multi-task Bias-Variance Trade-off Through Functional Constraints

Multi-task learning aims to acquire a set of functions, either regressors or classifiers, that perform well for diverse tasks. At its core, the idea behind multi-task learning is to exploit the intrinsic similarity across data sources to aid in the learning process for each individual domain. In this paper we draw intuition from the two extreme learning scenarios -- a single function for all tasks, and a task-specific function that ignores the other tasks dependencies -- to propose a bias-variance trade-off. To control the relationship between the variance (given by the number of i.i.d. samples), and the bias (coming from data from other task), we introduce a constrained learning formulation that enforces domain specific solutions to be close to a central function. This problem is solved in the dual domain, for which we propose a stochastic primal-dual algorithm. Experimental results for a multi-domain classification problem with real data show that the proposed procedure outperforms both the task specific, as well as the single classifiers.

Multi-task Supervised Learning via Cross-learning

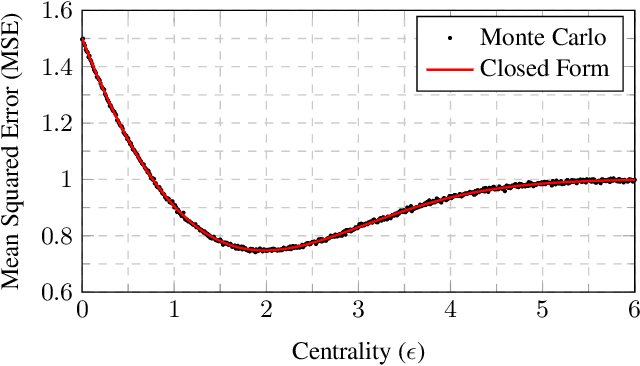
In this paper we consider a problem known as multi-task learning, consisting of fitting a set of classifier or regression functions intended for solving different tasks. In our novel formulation, we couple the parameters of these functions, so that they learn in their task specific domains while staying close to each other. This facilitates cross-fertilization in which data collected across different domains help improving the learning performance at each other task. First, we present a simplified case in which the goal is to estimate the means of two Gaussian variables, for the purpose of gaining some insights on the advantage of the proposed cross-learning strategy. Then we provide a stochastic projected gradient algorithm to perform cross-learning over a generic loss function. If the number of parameters is large, then the projection step becomes computationally expensive. To avoid this situation, we derive a primal-dual algorithm that exploits the structure of the dual problem, achieving a formulation whose complexity only depends on the number of tasks. Preliminary numerical experiments for image classification by neural networks trained on a dataset divided in different domains corroborate that the cross-learned function outperforms both the task-specific and the consensus approaches.

Policy Gradient for Continuing Tasks in Non-stationary Markov Decision Processes

Reinforcement learning considers the problem of finding policies that maximize an expected cumulative reward in a Markov decision process with unknown transition probabilities. In this paper we consider the problem of finding optimal policies assuming that they belong to a reproducing kernel Hilbert space (RKHS). To that end we compute unbiased stochastic gradients of the value function which we use as ascent directions to update the policy. A major drawback of policy gradient-type algorithms is that they are limited to episodic tasks unless stationarity assumptions are imposed. Hence preventing these algorithms to be fully implemented online, which is a desirable property for systems that need to adapt to new tasks and/or environments in deployment. The main requirement for a policy gradient algorithm to work is that the estimate of the gradient at any point in time is an ascent direction for the initial value function. In this work we establish that indeed this is the case which enables to show the convergence of the online algorithm to the critical points of the initial value function. A numerical example shows the ability of our online algorithm to learn to solve a navigation and surveillance problem, in which an agent must loop between to goal locations. This example corroborates our theoretical findings about the ascent directions of subsequent stochastic gradients. It also shows how the agent running our online algorithm succeeds in learning to navigate, following a continuing cyclic trajectory that does not comply with the standard stationarity assumptions in the literature for non episodic training.

Nonparametric Basis Pursuit via Sparse Kernel-based Learning

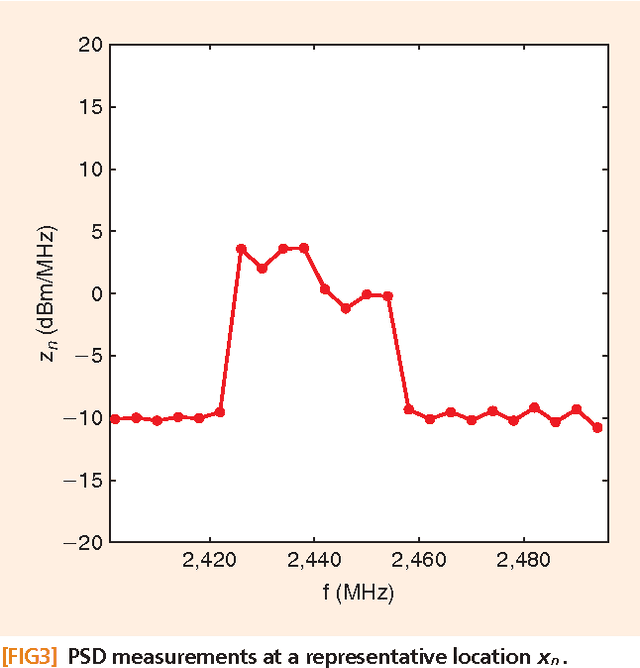
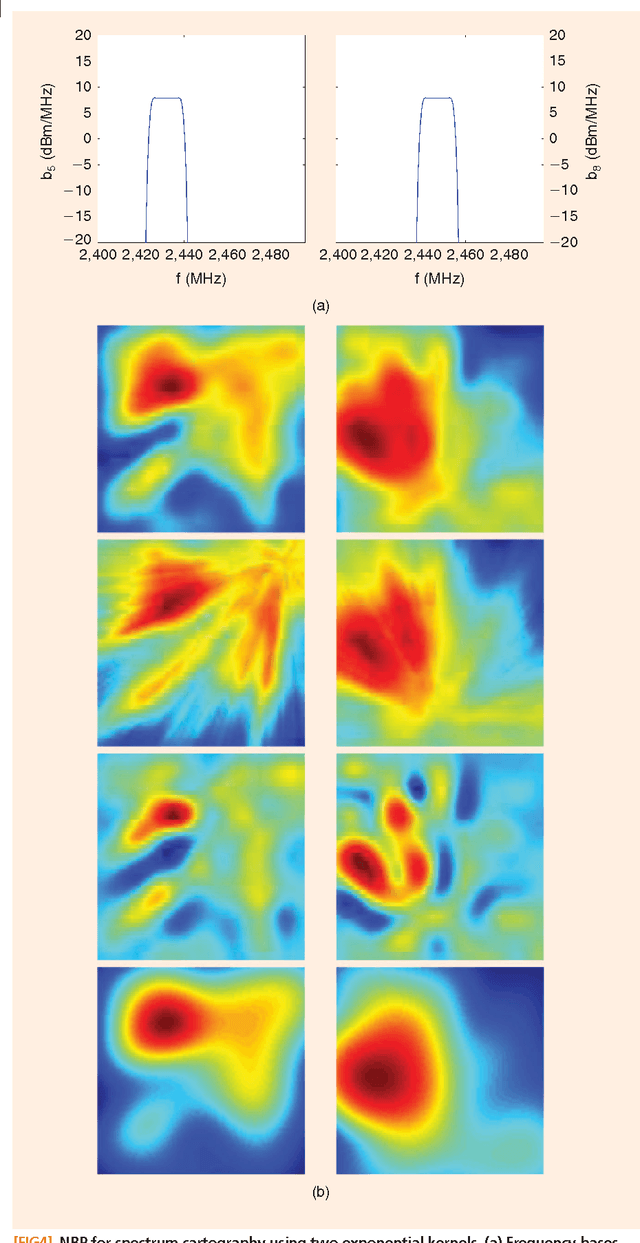
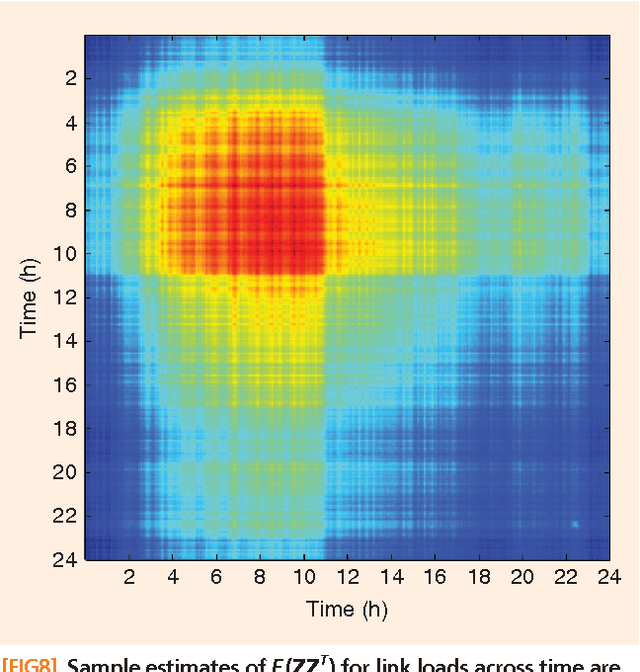
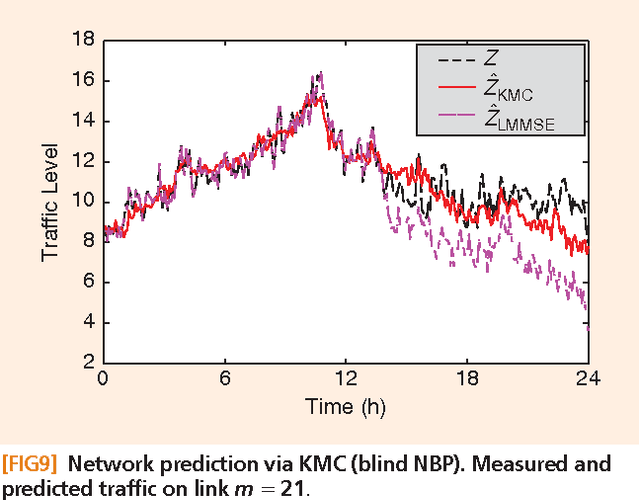
Signal processing tasks as fundamental as sampling, reconstruction, minimum mean-square error interpolation and prediction can be viewed under the prism of reproducing kernel Hilbert spaces. Endowing this vantage point with contemporary advances in sparsity-aware modeling and processing, promotes the nonparametric basis pursuit advocated in this paper as the overarching framework for the confluence of kernel-based learning (KBL) approaches leveraging sparse linear regression, nuclear-norm regularization, and dictionary learning. The novel sparse KBL toolbox goes beyond translating sparse parametric approaches to their nonparametric counterparts, to incorporate new possibilities such as multi-kernel selection and matrix smoothing. The impact of sparse KBL to signal processing applications is illustrated through test cases from cognitive radio sensing, microarray data imputation, and network traffic prediction.

Rank regularization and Bayesian inference for tensor completion and extrapolation

A novel regularizer of the PARAFAC decomposition factors capturing the tensor's rank is proposed in this paper, as the key enabler for completion of three-way data arrays with missing entries. Set in a Bayesian framework, the tensor completion method incorporates prior information to enhance its smoothing and prediction capabilities. This probabilistic approach can naturally accommodate general models for the data distribution, lending itself to various fitting criteria that yield optimum estimates in the maximum-a-posteriori sense. In particular, two algorithms are devised for Gaussian- and Poisson-distributed data, that minimize the rank-regularized least-squares error and Kullback-Leibler divergence, respectively. The proposed technique is able to recover the "ground-truth'' tensor rank when tested on synthetic data, and to complete brain imaging and yeast gene expression datasets with 50% and 15% of missing entries respectively, resulting in recovery errors at -10dB and -15dB.