Nonparametric Basis Pursuit via Sparse Kernel-based Learning
Paper and Code
Feb 21, 2013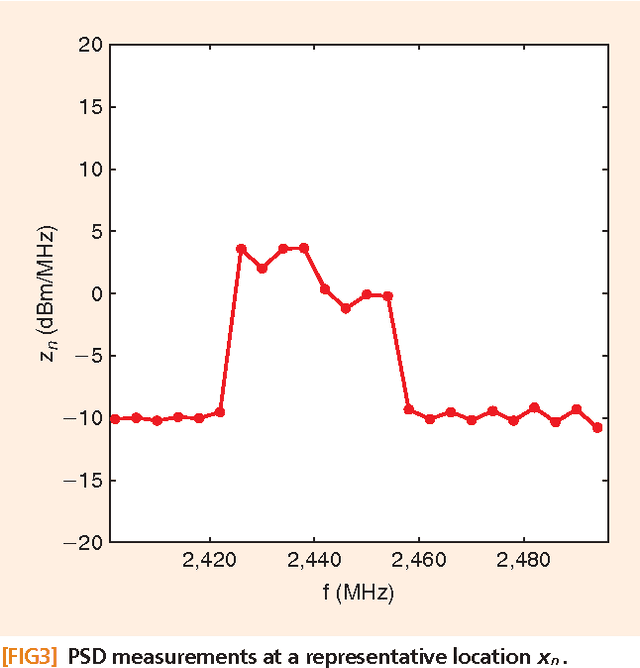
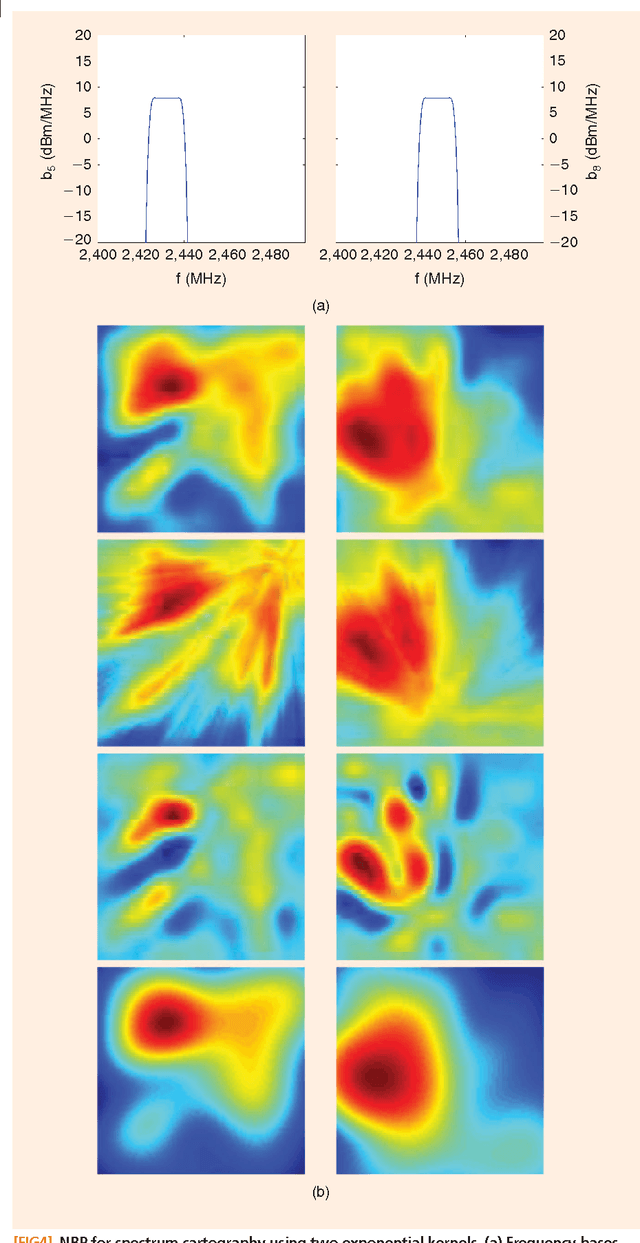
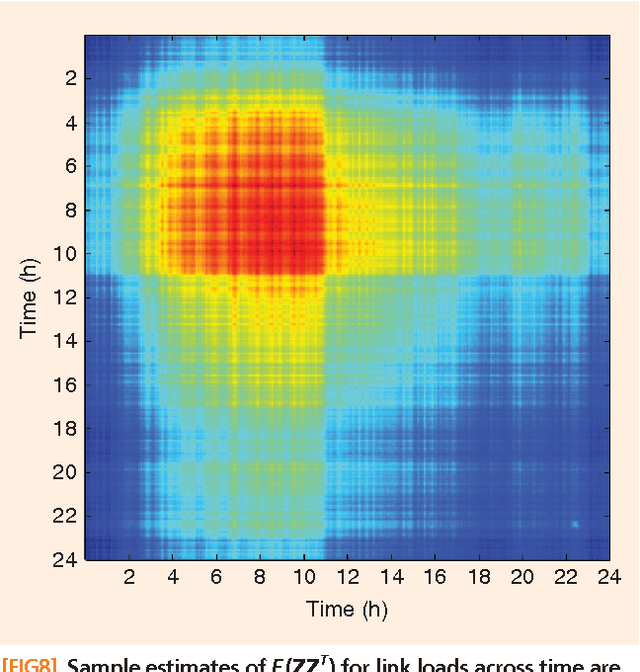
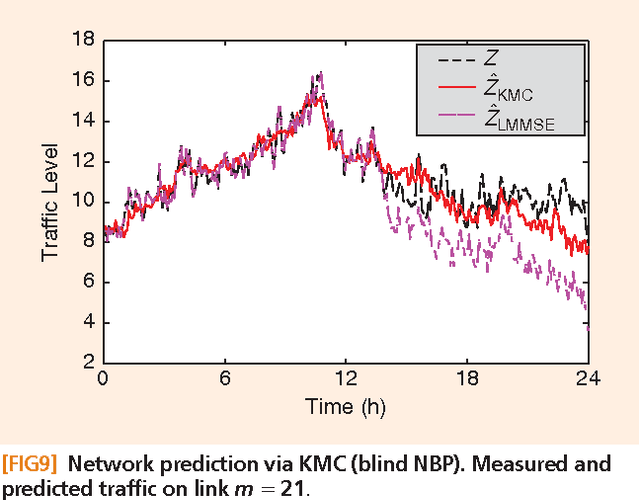
Signal processing tasks as fundamental as sampling, reconstruction, minimum mean-square error interpolation and prediction can be viewed under the prism of reproducing kernel Hilbert spaces. Endowing this vantage point with contemporary advances in sparsity-aware modeling and processing, promotes the nonparametric basis pursuit advocated in this paper as the overarching framework for the confluence of kernel-based learning (KBL) approaches leveraging sparse linear regression, nuclear-norm regularization, and dictionary learning. The novel sparse KBL toolbox goes beyond translating sparse parametric approaches to their nonparametric counterparts, to incorporate new possibilities such as multi-kernel selection and matrix smoothing. The impact of sparse KBL to signal processing applications is illustrated through test cases from cognitive radio sensing, microarray data imputation, and network traffic prediction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge