Graph-Aware Diffusion for Signal Generation

We study the problem of generating graph signals from unknown distributions defined over given graphs, relevant to domains such as recommender systems or sensor networks. Our approach builds on generative diffusion models, which are well established in vision and graph generation but remain underexplored for graph signals. Existing methods lack generality, either ignoring the graph structure in the forward process or designing graph-aware mechanisms tailored to specific domains. We adopt a forward process that incorporates the graph through the heat equation. Rather than relying on the standard formulation, we consider a time-warped coefficient to mitigate the exponential decay of the drift term, yielding a graph-aware generative diffusion model (GAD). We analyze its forward dynamics, proving convergence to a Gaussian Markov random field with covariance parametrized by the graph Laplacian, and interpret the backward dynamics as a sequence of graph-signal denoising problems. Finally, we demonstrate the advantages of GAD on synthetic data, real traffic speed measurements, and a temperature sensor network.

Precision Neural Networks: Joint Graph And Relational Learning

CoVariance Neural Networks (VNNs) perform convolutions on the graph determined by the covariance matrix of the data, which enables expressive and stable covariance-based learning. However, covariance matrices are typically dense, fail to encode conditional independence, and are often precomputed in a task-agnostic way, which may hinder performance. To overcome these limitations, we study Precision Neural Networks (PNNs), i.e., VNNs on the precision matrix -- the inverse covariance. The precision matrix naturally encodes statistical independence, often exhibits sparsity, and preserves the covariance spectral structure. To make precision estimation task-aware, we formulate an optimization problem that jointly learns the network parameters and the precision matrix, and solve it via alternating optimization, by sequentially updating the network weights and the precision estimate. We theoretically bound the distance between the estimated and true precision matrices at each iteration, and demonstrate the effectiveness of joint estimation compared to two-step approaches on synthetic and real-world data.

CoVariance Filters and Neural Networks over Hilbert Spaces

CoVariance Neural Networks (VNNs) perform graph convolutions on the empirical covariance matrix of signals defined over finite-dimensional Hilbert spaces, motivated by robustness and transferability properties. Yet, little is known about how these arguments extend to infinite-dimensional Hilbert spaces. In this work, we take a first step by introducing a novel convolutional learning framework for signals defined over infinite-dimensional Hilbert spaces, centered on the (empirical) covariance operator. We constructively define Hilbert coVariance Filters (HVFs) and design Hilbert coVariance Networks (HVNs) as stacks of HVF filterbanks with nonlinear activations. We propose a principled discretization procedure, and we prove that empirical HVFs can recover the Functional PCA (FPCA) of the filtered signals. We then describe the versatility of our framework with examples ranging from multivariate real-valued functions to reproducing kernel Hilbert spaces. Finally, we validate HVNs on both synthetic and real-world time-series classification tasks, showing robust performance compared to MLP and FPCA-based classifiers.

Graph signal aware decomposition of dynamic networks via latent graphs

Dynamics on and of networks refer to changes in topology and node-associated signals, respectively and are pervasive in many socio-technological systems, including social, biological, and infrastructure networks. Due to practical constraints, privacy concerns, or malfunctions, we often observe only a fraction of the topological evolution and associated signal, which not only hinders downstream tasks but also restricts our analysis of network evolution. Such aspects could be mitigated by moving our attention at the underlying latent driving factors of the network evolution, which can be naturally uncovered via low-rank tensor decomposition. Tensor-based methods provide a powerful means of uncovering the underlying factors of network evolution through low-rank decompositions. However, the extracted embeddings typically lack a relational structure and are obtained independently from the node signals. This disconnect reduces the interpretability of the embeddings and overlooks the coupling between topology and signals. To address these limitations, we propose a novel two-way decomposition to represent a dynamic graph topology, where the structural evolution is captured by a linear combination of latent graph adjacency matrices reflecting the overall joint evolution of both the topology and the signal. Using spatio-temporal data, we estimate the latent adjacency matrices and their temporal scaling signatures via alternating minimization, and prove that our approach converges to a stationary point. Numerical results show that the proposed method recovers individually and collectively expressive latent graphs, outperforming both standard tensor-based decompositions and signal-based topology identification methods in reconstructing the missing network especially when observations are limited.

Directed Semi-Simplicial Learning with Applications to Brain Activity Decoding

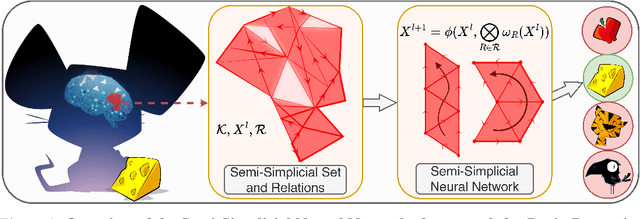
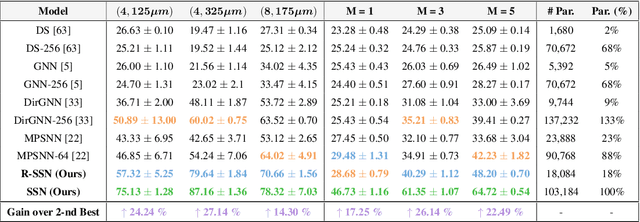
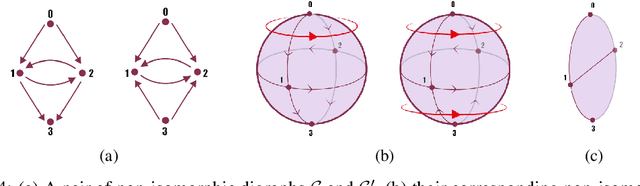
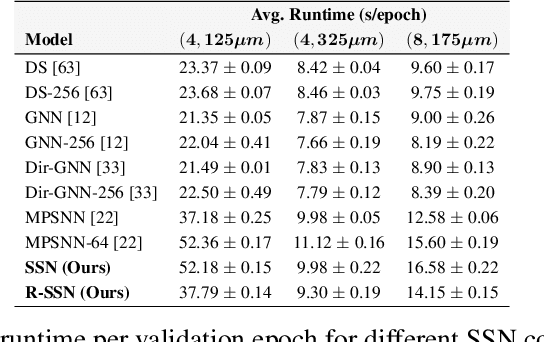
Graph Neural Networks (GNNs) excel at learning from pairwise interactions but often overlook multi-way and hierarchical relationships. Topological Deep Learning (TDL) addresses this limitation by leveraging combinatorial topological spaces. However, existing TDL models are restricted to undirected settings and fail to capture the higher-order directed patterns prevalent in many complex systems, e.g., brain networks, where such interactions are both abundant and functionally significant. To fill this gap, we introduce Semi-Simplicial Neural Networks (SSNs), a principled class of TDL models that operate on semi-simplicial sets -- combinatorial structures that encode directed higher-order motifs and their directional relationships. To enhance scalability, we propose Routing-SSNs, which dynamically select the most informative relations in a learnable manner. We prove that SSNs are strictly more expressive than standard graph and TDL models. We then introduce a new principled framework for brain dynamics representation learning, grounded in the ability of SSNs to provably recover topological descriptors shown to successfully characterize brain activity. Empirically, SSNs achieve state-of-the-art performance on brain dynamics classification tasks, outperforming the second-best model by up to 27%, and message passing GNNs by up to 50% in accuracy. Our results highlight the potential of principled topological models for learning from structured brain data, establishing a unique real-world case study for TDL. We also test SSNs on standard node classification and edge regression tasks, showing competitive performance. We will make the code and data publicly available.

Matched Topological Subspace Detector

Topological spaces, represented by simplicial complexes, capture richer relationships than graphs by modeling interactions not only between nodes but also among higher-order entities, such as edges or triangles. This motivates the representation of information defined in irregular domains as topological signals. By leveraging the spectral dualities of Hodge and Dirac theory, practical topological signals often concentrate in specific spectral subspaces (e.g., gradient or curl). For instance, in a foreign currency exchange network, the exchange flow signals typically satisfy the arbitrage-free condition and hence are curl-free. However, the presence of anomalies can disrupt these conditions, causing the signals to deviate from such subspaces. In this work, we formulate a hypothesis testing framework to detect whether simplicial complex signals lie in specific subspaces in a principled and tractable manner. Concretely, we propose Neyman-Pearson matched topological subspace detectors for signals defined at a single simplicial level (such as edges) or jointly across all levels of a simplicial complex. The (energy-based projection) proposed detectors handle missing values, provide closed-form performance analysis, and effectively capture the unique topological properties of the data. We demonstrate the effectiveness of the proposed topological detectors on various real-world data, including foreign currency exchange networks.

Towards Carbon Footprint-Aware Recommender Systems for Greener Item Recommendation

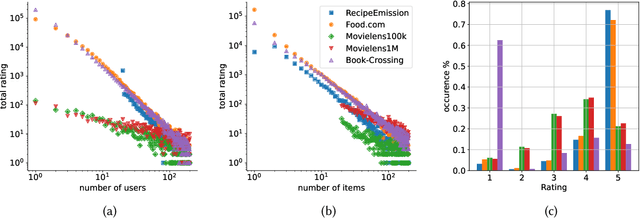
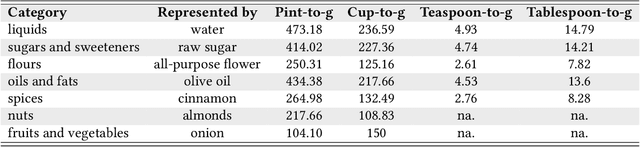
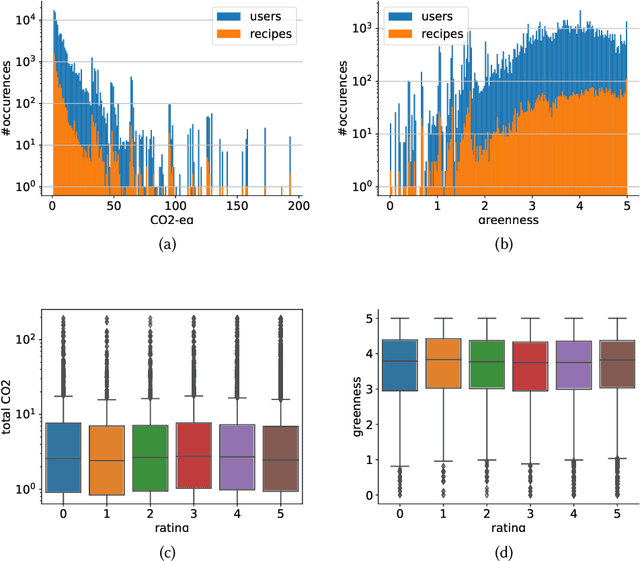
The commodity and widespread use of online shopping are having an unprecedented impact on climate, with emission figures from key actors that are easily comparable to those of a large-scale metropolis. Despite online shopping being fueled by recommender systems (RecSys) algorithms, the role and potential of the latter in promoting more sustainable choices is little studied. One of the main reasons for this could be attributed to the lack of a dataset containing carbon footprint emissions for the items. While building such a dataset is a rather challenging task, its presence is pivotal for opening the doors to novel perspectives, evaluations, and methods for RecSys research. In this paper, we target this bottleneck and study the environmental role of RecSys algorithms. First, we mine a dataset that includes carbon footprint emissions for its items. Then, we benchmark conventional RecSys algorithms in terms of accuracy and sustainability as two faces of the same coin. We find that RecSys algorithms optimized for accuracy overlook greenness and that longer recommendation lists are greener but less accurate. Then, we show that a simple reranking approach that accounts for the item's carbon footprint can establish a better trade-off between accuracy and greenness. This reranking approach is modular, ready to use, and can be applied to any RecSys algorithm without the need to alter the underlying mechanisms or retrain models. Our results show that a small sacrifice of accuracy can lead to significant improvements of recommendation greenness across all algorithms and list lengths. Arguably, this accuracy-greenness trade-off could even be seen as an enhancement of user satisfaction, particularly for purpose-driven users who prioritize the environmental impact of their choices. We anticipate this work will serve as the starting point for studying RecSys for more sustainable recommendations.

Topological Signal Processing and Learning: Recent Advances and Future Challenges

Developing methods to process irregularly structured data is crucial in applications like gene-regulatory, brain, power, and socioeconomic networks. Graphs have been the go-to algebraic tool for modeling the structure via nodes and edges capturing their interactions, leading to the establishment of the fields of graph signal processing (GSP) and graph machine learning (GML). Key graph-aware methods include Fourier transform, filtering, sampling, as well as topology identification and spatiotemporal processing. Although versatile, graphs can model only pairwise dependencies in the data. To this end, topological structures such as simplicial and cell complexes have emerged as algebraic representations for more intricate structure modeling in data-driven systems, fueling the rapid development of novel topological-based processing and learning methods. This paper first presents the core principles of topological signal processing through the Hodge theory, a framework instrumental in propelling the field forward thanks to principled connections with GSP-GML. It then outlines advances in topological signal representation, filtering, and sampling, as well as inferring topological structures from data, processing spatiotemporal topological signals, and connections with topological machine learning. The impact of topological signal processing and learning is finally highlighted in applications dealing with flow data over networks, geometric processing, statistical ranking, biology, and semantic communication.

Sparse Covariance Neural Networks

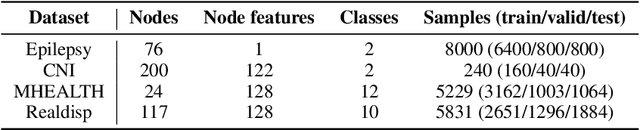
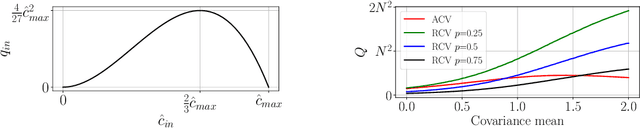
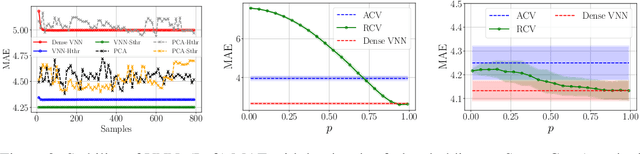
Covariance Neural Networks (VNNs) perform graph convolutions on the covariance matrix of tabular data and achieve success in a variety of applications. However, the empirical covariance matrix on which the VNNs operate may contain many spurious correlations, making VNNs' performance inconsistent due to these noisy estimates and decreasing their computational efficiency. To tackle this issue, we put forth Sparse coVariance Neural Networks (S-VNNs), a framework that applies sparsification techniques on the sample covariance matrix before convolution. When the true covariance matrix is sparse, we propose hard and soft thresholding to improve covariance estimation and reduce computational cost. Instead, when the true covariance is dense, we propose stochastic sparsification where data correlations are dropped in probability according to principled strategies. We show that S-VNNs are more stable than nominal VNNs as well as sparse principal component analysis. By analyzing the impact of sparsification on their behavior, we provide novel connections between S-VNN stability and data distribution. We support our theoretical findings with experimental results on various application scenarios, ranging from brain data to human action recognition, and show an improved task performance, stability, and computational efficiency of S-VNNs compared with nominal VNNs.

Spatiotemporal Covariance Neural Networks

Modeling spatiotemporal interactions in multivariate time series is key to their effective processing, but challenging because of their irregular and often unknown structure. Statistical properties of the data provide useful biases to model interdependencies and are leveraged by correlation and covariance-based networks as well as by processing pipelines relying on principal component analysis (PCA). However, PCA and its temporal extensions suffer instabilities in the covariance eigenvectors when the corresponding eigenvalues are close to each other, making their application to dynamic and streaming data settings challenging. To address these issues, we exploit the analogy between PCA and graph convolutional filters to introduce the SpatioTemporal coVariance Neural Network (STVNN), a relational learning model that operates on the sample covariance matrix of the time series and leverages joint spatiotemporal convolutions to model the data. To account for the streaming and non-stationary setting, we consider an online update of the parameters and sample covariance matrix. We prove the STVNN is stable to the uncertainties introduced by these online estimations, thus improving over temporal PCA-based methods. Experimental results corroborate our theoretical findings and show that STVNN is competitive for multivariate time series processing, it adapts to changes in the data distribution, and it is orders of magnitude more stable than online temporal PCA.