Stochastic Sequential Decision Making over Expanding Networks with Graph Filtering

Graph filters leverage topological information to process networked data with existing methods mainly studying fixed graphs, ignoring that graphs often expand as nodes continually attach with an unknown pattern. The latter requires developing filter-based decision-making paradigms that take evolution and uncertainty into account. Existing approaches rely on either pre-designed filters or online learning, limited to a myopic view considering only past or present information. To account for future impacts, we propose a stochastic sequential decision-making framework for filtering networked data with a policy that adapts filtering to expanding graphs. By representing filter shifts as agents, we model the filter as a multi-agent system and train the policy following multi-agent reinforcement learning. This accounts for long-term rewards and captures expansion dynamics through sequential decision-making. Moreover, we develop a context-aware graph neural network to parameterize the policy, which tunes filter parameters based on information of both the graph and agents. Experiments on synthetic and real datasets from cold-start recommendation to COVID prediction highlight the benefits of using a sequential decision-making perspective over batch and online filtering alternatives.

Graph signal aware decomposition of dynamic networks via latent graphs

Dynamics on and of networks refer to changes in topology and node-associated signals, respectively and are pervasive in many socio-technological systems, including social, biological, and infrastructure networks. Due to practical constraints, privacy concerns, or malfunctions, we often observe only a fraction of the topological evolution and associated signal, which not only hinders downstream tasks but also restricts our analysis of network evolution. Such aspects could be mitigated by moving our attention at the underlying latent driving factors of the network evolution, which can be naturally uncovered via low-rank tensor decomposition. Tensor-based methods provide a powerful means of uncovering the underlying factors of network evolution through low-rank decompositions. However, the extracted embeddings typically lack a relational structure and are obtained independently from the node signals. This disconnect reduces the interpretability of the embeddings and overlooks the coupling between topology and signals. To address these limitations, we propose a novel two-way decomposition to represent a dynamic graph topology, where the structural evolution is captured by a linear combination of latent graph adjacency matrices reflecting the overall joint evolution of both the topology and the signal. Using spatio-temporal data, we estimate the latent adjacency matrices and their temporal scaling signatures via alternating minimization, and prove that our approach converges to a stationary point. Numerical results show that the proposed method recovers individually and collectively expressive latent graphs, outperforming both standard tensor-based decompositions and signal-based topology identification methods in reconstructing the missing network especially when observations are limited.

Online Learning Of Expanding Graphs

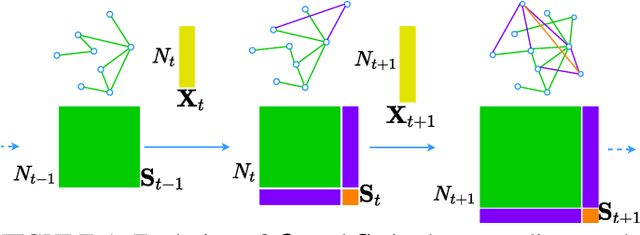
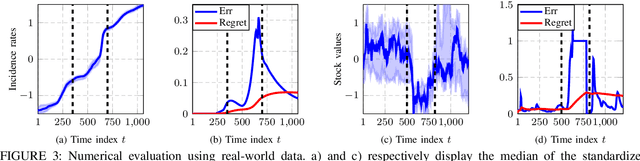
This paper addresses the problem of online network topology inference for expanding graphs from a stream of spatiotemporal signals. Online algorithms for dynamic graph learning are crucial in delay-sensitive applications or when changes in topology occur rapidly. While existing works focus on inferring the connectivity within a fixed set of nodes, in practice, the graph can grow as new nodes join the network. This poses additional challenges like modeling temporal dynamics involving signals and graphs of different sizes. This growth also increases the computational complexity of the learning process, which may become prohibitive. To the best of our knowledge, this is the first work to tackle this setting. We propose a general online algorithm based on projected proximal gradient descent that accounts for the increasing graph size at each iteration. Recursively updating the sample covariance matrix is a key aspect of our approach. We introduce a strategy that enables different types of updates for nodes that just joined the network and for previously existing nodes. To provide further insights into the proposed method, we specialize it in Gaussian Markov random field settings, where we analyze the computational complexity and characterize the dynamic cumulative regret. Finally, we demonstrate the effectiveness of the proposed approach using both controlled experiments and real-world datasets from epidemic and financial networks.

Online Graph Filtering Over Expanding Graphs

Graph filters are a staple tool for processing signals over graphs in a multitude of downstream tasks. However, they are commonly designed for graphs with a fixed number of nodes, despite real-world networks typically grow over time. This topological evolution is often known up to a stochastic model, thus, making conventional graph filters ill-equipped to withstand such topological changes, their uncertainty, as well as the dynamic nature of the incoming data. To tackle these issues, we propose an online graph filtering framework by relying on online learning principles. We design filters for scenarios where the topology is both known and unknown, including a learner adaptive to such evolution. We conduct a regret analysis to highlight the role played by the different components such as the online algorithm, the filter order, and the growing graph model. Numerical experiments with synthetic and real data corroborate the proposed approach for graph signal inference tasks and show a competitive performance w.r.t. baselines and state-of-the-art alternatives.

Online Filtering over Expanding Graphs

Data processing tasks over graphs couple the data residing over the nodes with the topology through graph signal processing tools. Graph filters are one such prominent tool, having been used in applications such as denoising, interpolation, and classification. However, they are mainly used on fixed graphs although many networks grow in practice, with nodes continually attaching to the topology. Re-training the filter every time a new node attaches is computationally demanding; hence an online learning solution that adapts to the evolving graph is needed. We propose an online update of the filter, based on the principles of online machine learning. To update the filter, we perform online gradient descent, which has a provable regret bound with respect to the filter computed offline. We show the performance of our method for signal interpolation at the incoming nodes. Numerical results on synthetic and graph-based recommender systems show that the proposed approach compares well to the offline baseline filter while outperforming competitive approaches. These findings lay the foundation for efficient filtering over expanding graphs.

Graph filtering over expanding graphs

Our capacity to learn representations from data is related to our ability to design filters that can leverage their coupling with the underlying domain. Graph filters are one such tool for network data and have been used in a myriad of applications. But graph filters work only with a fixed number of nodes despite the expanding nature of practical networks. Learning filters in this setting is challenging not only because of the increased dimensions but also because the connectivity is known only up to an attachment model. We propose a filter learning scheme for data over expanding graphs by relying only on such a model. By characterizing the filter stochastically, we develop an empirical risk minimization framework inspired by multi-kernel learning to balance the information inflow and outflow at the incoming nodes. We particularize the approach for denoising and semi-supervised learning (SSL) over expanding graphs and show near-optimal performance compared with baselines relying on the exact topology. For SSL, the proposed scheme uses the incoming node information to improve the task on the existing ones. These findings lay the foundation for learning representations over expanding graphs by relying only on the stochastic connectivity model.

Learning Expanding Graphs for Signal Interpolation

Performing signal processing over graphs requires knowledge of the underlying fixed topology. However, graphs often grow in size with new nodes appearing over time, whose connectivity is typically unknown; hence, making more challenging the downstream tasks in applications like cold start recommendation. We address such a challenge for signal interpolation at the incoming nodes blind to the topological connectivity of the specific node. Specifically, we propose a stochastic attachment model for incoming nodes parameterized by the attachment probabilities and edge weights. We estimate these parameters in a data-driven fashion by relying only on the attachment behaviour of earlier incoming nodes with the goal of interpolating the signal value. We study the non-convexity of the problem at hand, derive conditions when it can be marginally convexified, and propose an alternating projected descent approach between estimating the attachment probabilities and the edge weights. Numerical experiments with synthetic and real data dealing in cold start collaborative filtering corroborate our findings.