Topological Signal Processing and Learning: Recent Advances and Future Challenges

Developing methods to process irregularly structured data is crucial in applications like gene-regulatory, brain, power, and socioeconomic networks. Graphs have been the go-to algebraic tool for modeling the structure via nodes and edges capturing their interactions, leading to the establishment of the fields of graph signal processing (GSP) and graph machine learning (GML). Key graph-aware methods include Fourier transform, filtering, sampling, as well as topology identification and spatiotemporal processing. Although versatile, graphs can model only pairwise dependencies in the data. To this end, topological structures such as simplicial and cell complexes have emerged as algebraic representations for more intricate structure modeling in data-driven systems, fueling the rapid development of novel topological-based processing and learning methods. This paper first presents the core principles of topological signal processing through the Hodge theory, a framework instrumental in propelling the field forward thanks to principled connections with GSP-GML. It then outlines advances in topological signal representation, filtering, and sampling, as well as inferring topological structures from data, processing spatiotemporal topological signals, and connections with topological machine learning. The impact of topological signal processing and learning is finally highlighted in applications dealing with flow data over networks, geometric processing, statistical ranking, biology, and semantic communication.

Efficient Interpretable Nonlinear Modeling for Multiple Time Series

Predictive linear and nonlinear models based on kernel machines or deep neural networks have been used to discover dependencies among time series. This paper proposes an efficient nonlinear modeling approach for multiple time series, with a complexity comparable to linear vector autoregressive (VAR) models while still incorporating nonlinear interactions among different time-series variables. The modeling assumption is that the set of time series is generated in two steps: first, a linear VAR process in a latent space, and second, a set of invertible and Lipschitz continuous nonlinear mappings that are applied per sensor, that is, a component-wise mapping from each latent variable to a variable in the measurement space. The VAR coefficient identification provides a topology representation of the dependencies among the aforementioned variables. The proposed approach models each component-wise nonlinearity using an invertible neural network and imposes sparsity on the VAR coefficients to reflect the parsimonious dependencies usually found in real applications. To efficiently solve the formulated optimization problems, a custom algorithm is devised combining proximal gradient descent, stochastic primal-dual updates, and projection to enforce the corresponding constraints. Experimental results on both synthetic and real data sets show that the proposed algorithm improves the identification of the support of the VAR coefficients in a parsimonious manner while also improving the time-series prediction, as compared to the current state-of-the-art methods.

Zero-delay Consistent Signal Reconstruction from Streamed Multivariate Time Series

Digitalizing real-world analog signals typically involves sampling in time and discretizing in amplitude. Subsequent signal reconstructions inevitably incur an error that depends on the amplitude resolution and the temporal density of the acquired samples. From an implementation viewpoint, consistent signal reconstruction methods have proven a profitable error-rate decay as the sampling rate increases. Despite that, these results are obtained under offline settings. Therefore, a research gap exists regarding methods for consistent signal reconstruction from data streams. This paper presents a method that consistently reconstructs streamed multivariate time series of quantization intervals under a zero-delay response requirement. On the other hand, previous work has shown that the temporal dependencies within univariate time series can be exploited to reduce the roughness of zero-delay signal reconstructions. This work shows that the spatiotemporal dependencies within multivariate time series can also be exploited to achieve improved results. Specifically, the spatiotemporal dependencies of the multivariate time series are learned, with the assistance of a recurrent neural network, to reduce the roughness of the signal reconstruction on average while ensuring consistency. Our experiments show that our proposed method achieves a favorable error-rate decay with the sampling rate compared to a similar but non-consistent reconstruction.

An Online Multiple Kernel Parallelizable Learning Scheme

The performance of reproducing kernel Hilbert space-based methods is known to be sensitive to the choice of the reproducing kernel. Choosing an adequate reproducing kernel can be challenging and computationally demanding, especially in data-rich tasks without prior information about the solution domain. In this paper, we propose a learning scheme that scalably combines several single kernel-based online methods to reduce the kernel-selection bias. The proposed learning scheme applies to any task formulated as a regularized empirical risk minimization convex problem. More specifically, our learning scheme is based on a multi-kernel learning formulation that can be applied to widen any single-kernel solution space, thus increasing the possibility of finding higher-performance solutions. In addition, it is parallelizable, allowing for the distribution of the computational load across different computing units. We show experimentally that the proposed learning scheme outperforms the combined single-kernel online methods separately in terms of the cumulative regularized least squares cost metric.

Zero-delay Consistent and Smooth Trainable Interpolation

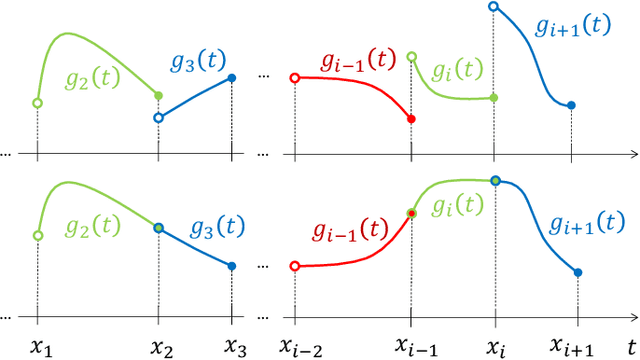
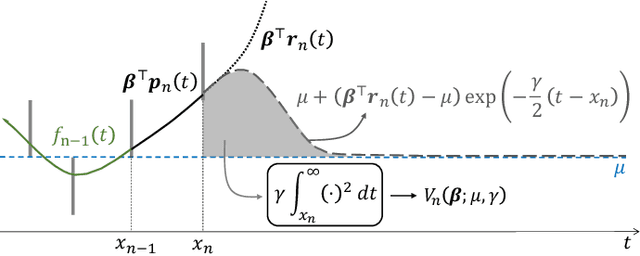
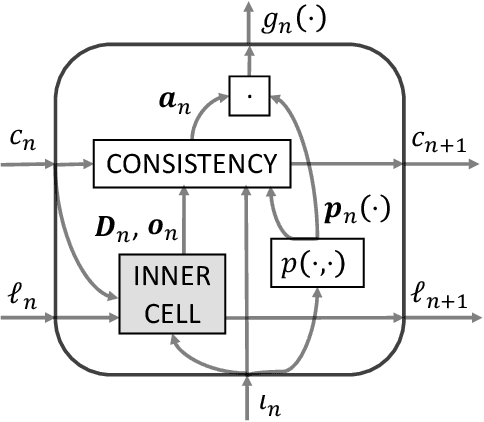
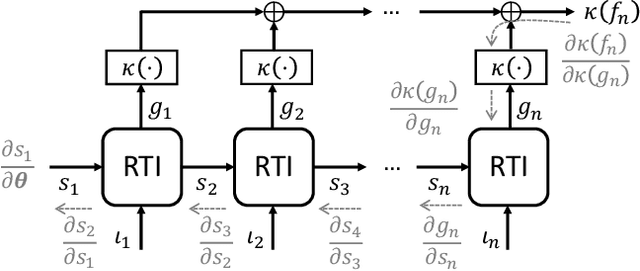
The question of how to produce a smooth interpolating curve from a stream of data points is addressed in this paper. To this end, we formalize the concept of real-time interpolator (RTI): a trainable unit that recovers smooth signals that are consistent with the received input samples in an online manner. Specifically, an RTI works under the requirement of producing a function section immediately after a sample is received (zero delay), without changing the reconstructed signal in past time sections. This work formulates the design of spline-based RTIs as a bi-level optimization problem. Their training consists in minimizing the average curvature of the interpolated signals over a set of example sequences. The latter are representative of the nature of the data sequence to be interpolated, allowing to tailor the RTI to a specific signal source. Our overall design allows for different possible schemes. In this work, we present two approaches, namely, the parametrized RTI and the recurrent neural network (RNN)-based RTI, including their architecture and properties. Experimental results show that the two proposed RTIs can be trained in a data-driven fashion to achieve improved performance (in terms of the curvature loss metric) with respect to a myopic-type RTI that only exploits the local information at each time sample, while maintaining smooth, zero-delay, and consistency requirements.

Random Feature Approximation for Online Nonlinear Graph Topology Identification

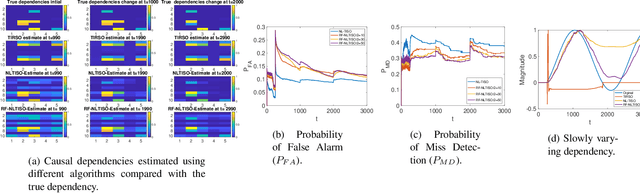
Online topology estimation of graph-connected time series is challenging, especially since the causal dependencies in many real-world networks are nonlinear. In this paper, we propose a kernel-based algorithm for graph topology estimation. The algorithm uses a Fourier-based Random feature approximation to tackle the curse of dimensionality associated with the kernel representations. Exploiting the fact that the real-world networks often exhibit sparse topologies, we propose a group lasso based optimization framework, which is solve using an iterative composite objective mirror descent method, yielding an online algorithm with fixed computational complexity per iteration. The experiments conducted on real and synthetic data show that the proposed method outperforms its competitors.

Explainable nonlinear modelling of multiple time series with invertible neural networks

A method for nonlinear topology identification is proposed, based on the assumption that a collection of time series are generated in two steps: i) a vector autoregressive process in a latent space, and ii) a nonlinear, component-wise, monotonically increasing observation mapping. The latter mappings are assumed invertible, and are modelled as shallow neural networks, so that their inverse can be numerically evaluated, and their parameters can be learned using a technique inspired in deep learning. Due to the function inversion, the back-propagation step is not straightforward, and this paper explains the steps needed to calculate the gradients applying implicit differentiation. Whereas the model explainability is the same as that for linear VAR processes, preliminary numerical tests show that the prediction error becomes smaller.

Online Non-linear Topology Identification from Graph-connected Time Series

Estimating the unknown causal dependencies among graph-connected time series plays an important role in many applications, such as sensor network analysis, signal processing over cyber-physical systems, and finance engineering. Inference of such causal dependencies, often know as topology identification, is not well studied for non-linear non-stationary systems, and most of the existing methods are batch-based which are not capable of handling streaming sensor signals. In this paper, we propose an online kernel-based algorithm for topology estimation of non-linear vector autoregressive time series by solving a sparse online optimization framework using the composite objective mirror descent method. Experiments conducted on real and synthetic data sets show that the proposed algorithm outperforms the state-of-the-art methods for topology estimation.

Channel Gain Cartography via Mixture of Experts

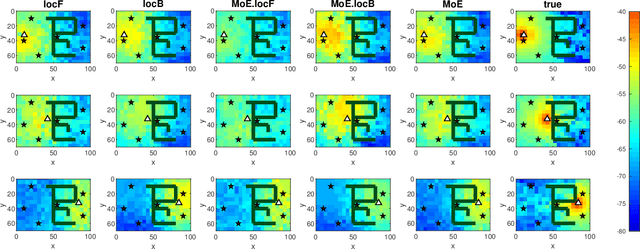
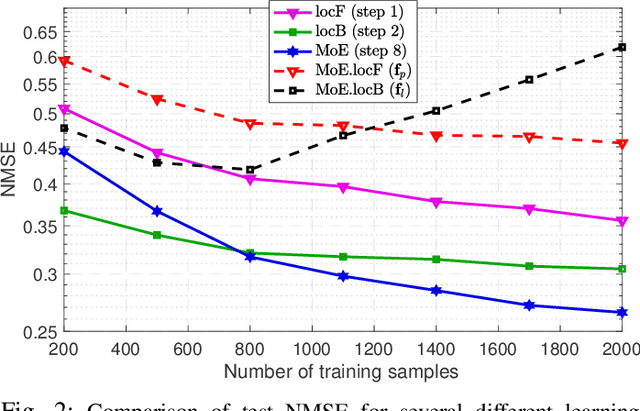
In order to estimate the channel gain (CG) between the locations of an arbitrary transceiver pair across a geographic area of interest, CG maps can be constructed from spatially distributed sensor measurements. Most approaches to build such spectrum maps are location-based, meaning that the input variable to the estimating function is a pair of spatial locations. The performance of such maps depends critically on the ability of the sensors to determine their positions, which may be drastically impaired if the positioning pilot signals are affected by multi-path channels. An alternative location-free approach was recently proposed for spectrum power maps, where the input variable to the maps consists of features extracted from the positioning signals, instead of location estimates. The location-based and the location-free approaches have complementary merits. In this work, apart from adapting the location-free features for the CG maps, a method that can combine both approaches is proposed in a mixture-of-experts framework.

Online Hyperparameter Search Interleaved with Proximal Parameter Updates

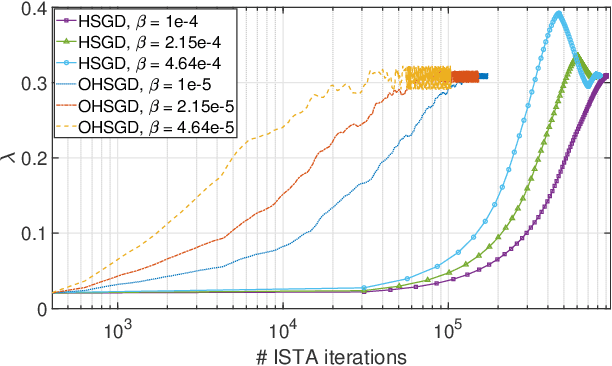
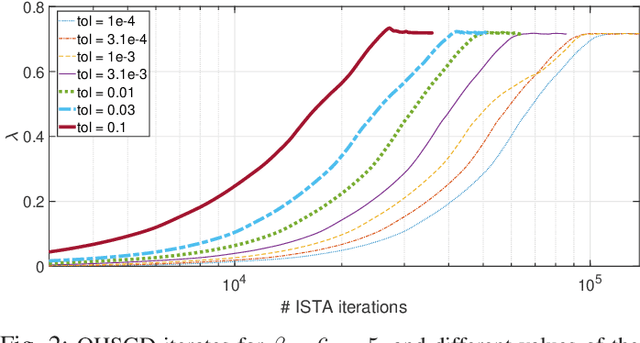
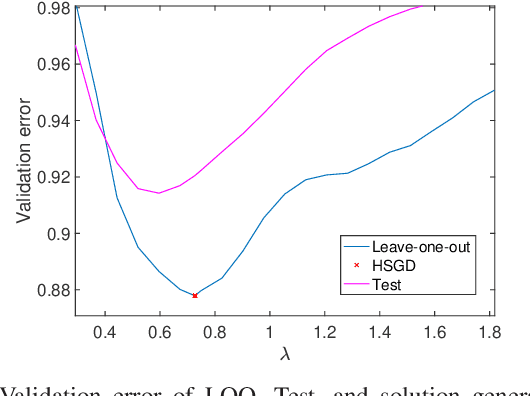
There is a clear need for efficient algorithms to tune hyperparameters for statistical learning schemes, since the commonly applied search methods (such as grid search with N-fold cross-validation) are inefficient and/or approximate. Previously existing algorithms that efficiently search for hyperparameters relying on the smoothness of the cost function cannot be applied in problems such as Lasso regression. In this contribution, we develop a hyperparameter optimization method that relies on the structure of proximal gradient methods and does not require a smooth cost function. Such a method is applied to Leave-one-out (LOO)-validated Lasso and Group Lasso to yield efficient, data-driven, hyperparameter optimization algorithms. Numerical experiments corroborate the convergence of the proposed method to a local optimum of the LOO validation error curve, and the efficiency of its approximations.