Emilio Ruiz-Moreno
Zero-delay Consistent Signal Reconstruction from Streamed Multivariate Time Series
Aug 23, 2023Abstract:Digitalizing real-world analog signals typically involves sampling in time and discretizing in amplitude. Subsequent signal reconstructions inevitably incur an error that depends on the amplitude resolution and the temporal density of the acquired samples. From an implementation viewpoint, consistent signal reconstruction methods have proven a profitable error-rate decay as the sampling rate increases. Despite that, these results are obtained under offline settings. Therefore, a research gap exists regarding methods for consistent signal reconstruction from data streams. This paper presents a method that consistently reconstructs streamed multivariate time series of quantization intervals under a zero-delay response requirement. On the other hand, previous work has shown that the temporal dependencies within univariate time series can be exploited to reduce the roughness of zero-delay signal reconstructions. This work shows that the spatiotemporal dependencies within multivariate time series can also be exploited to achieve improved results. Specifically, the spatiotemporal dependencies of the multivariate time series are learned, with the assistance of a recurrent neural network, to reduce the roughness of the signal reconstruction on average while ensuring consistency. Our experiments show that our proposed method achieves a favorable error-rate decay with the sampling rate compared to a similar but non-consistent reconstruction.
An Online Multiple Kernel Parallelizable Learning Scheme
Aug 19, 2023

Abstract:The performance of reproducing kernel Hilbert space-based methods is known to be sensitive to the choice of the reproducing kernel. Choosing an adequate reproducing kernel can be challenging and computationally demanding, especially in data-rich tasks without prior information about the solution domain. In this paper, we propose a learning scheme that scalably combines several single kernel-based online methods to reduce the kernel-selection bias. The proposed learning scheme applies to any task formulated as a regularized empirical risk minimization convex problem. More specifically, our learning scheme is based on a multi-kernel learning formulation that can be applied to widen any single-kernel solution space, thus increasing the possibility of finding higher-performance solutions. In addition, it is parallelizable, allowing for the distribution of the computational load across different computing units. We show experimentally that the proposed learning scheme outperforms the combined single-kernel online methods separately in terms of the cumulative regularized least squares cost metric.
Zero-delay Consistent and Smooth Trainable Interpolation
Mar 07, 2022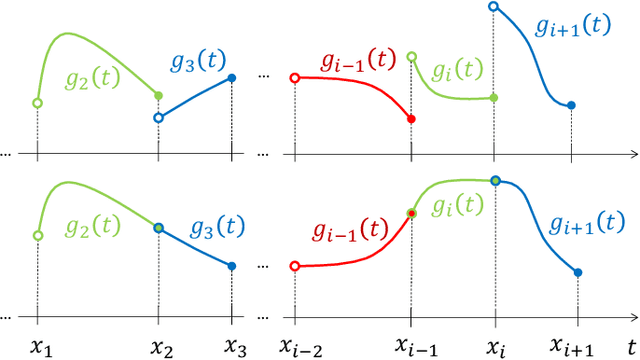
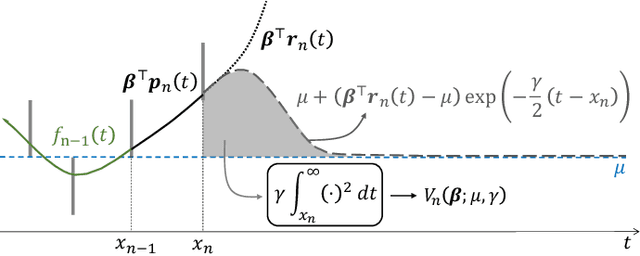
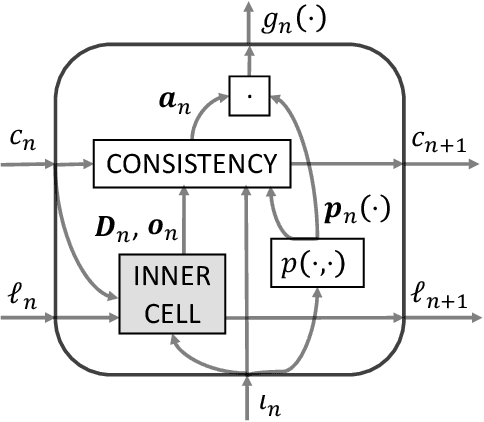
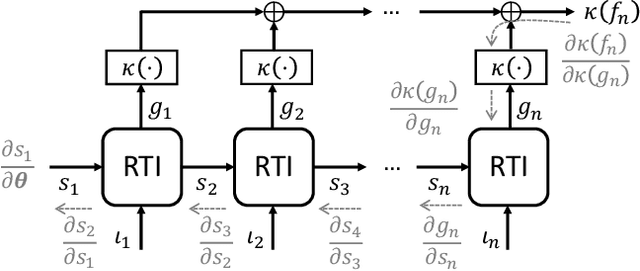
Abstract:The question of how to produce a smooth interpolating curve from a stream of data points is addressed in this paper. To this end, we formalize the concept of real-time interpolator (RTI): a trainable unit that recovers smooth signals that are consistent with the received input samples in an online manner. Specifically, an RTI works under the requirement of producing a function section immediately after a sample is received (zero delay), without changing the reconstructed signal in past time sections. This work formulates the design of spline-based RTIs as a bi-level optimization problem. Their training consists in minimizing the average curvature of the interpolated signals over a set of example sequences. The latter are representative of the nature of the data sequence to be interpolated, allowing to tailor the RTI to a specific signal source. Our overall design allows for different possible schemes. In this work, we present two approaches, namely, the parametrized RTI and the recurrent neural network (RNN)-based RTI, including their architecture and properties. Experimental results show that the two proposed RTIs can be trained in a data-driven fashion to achieve improved performance (in terms of the curvature loss metric) with respect to a myopic-type RTI that only exploits the local information at each time sample, while maintaining smooth, zero-delay, and consistency requirements.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge