Zero-delay Consistent and Smooth Trainable Interpolation

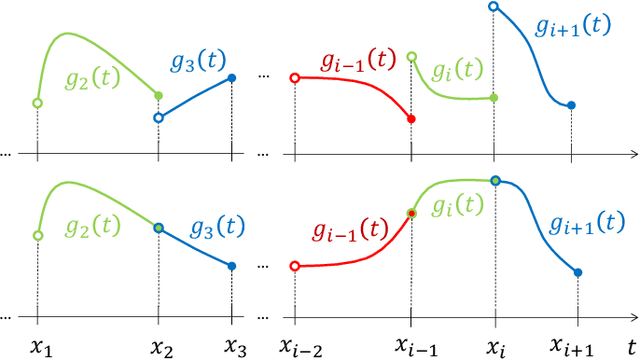
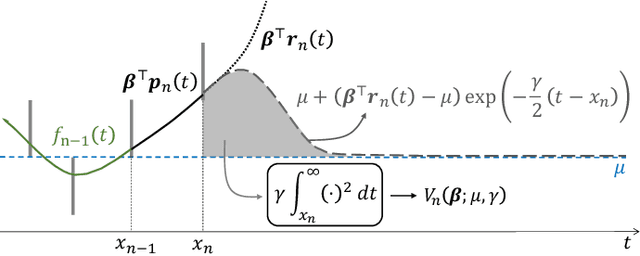
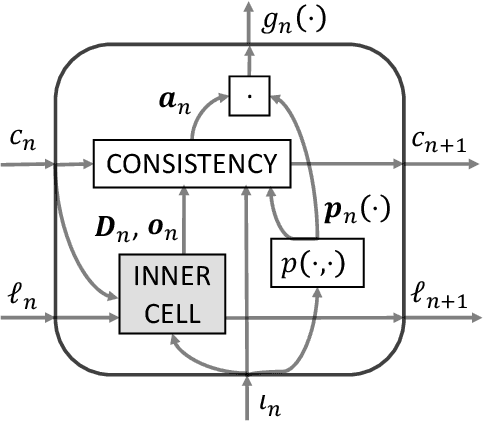
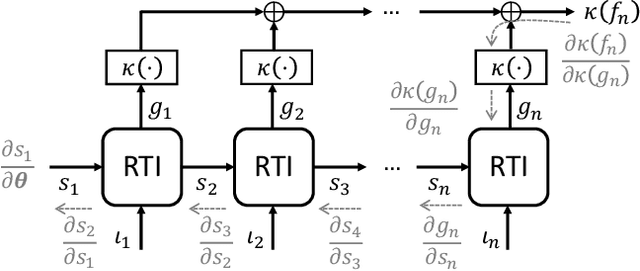
The question of how to produce a smooth interpolating curve from a stream of data points is addressed in this paper. To this end, we formalize the concept of real-time interpolator (RTI): a trainable unit that recovers smooth signals that are consistent with the received input samples in an online manner. Specifically, an RTI works under the requirement of producing a function section immediately after a sample is received (zero delay), without changing the reconstructed signal in past time sections. This work formulates the design of spline-based RTIs as a bi-level optimization problem. Their training consists in minimizing the average curvature of the interpolated signals over a set of example sequences. The latter are representative of the nature of the data sequence to be interpolated, allowing to tailor the RTI to a specific signal source. Our overall design allows for different possible schemes. In this work, we present two approaches, namely, the parametrized RTI and the recurrent neural network (RNN)-based RTI, including their architecture and properties. Experimental results show that the two proposed RTIs can be trained in a data-driven fashion to achieve improved performance (in terms of the curvature loss metric) with respect to a myopic-type RTI that only exploits the local information at each time sample, while maintaining smooth, zero-delay, and consistency requirements.