Rohan Money
Random Feature Approximation for Online Nonlinear Graph Topology Identification
Oct 19, 2021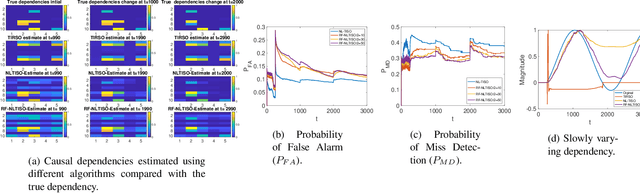

Abstract:Online topology estimation of graph-connected time series is challenging, especially since the causal dependencies in many real-world networks are nonlinear. In this paper, we propose a kernel-based algorithm for graph topology estimation. The algorithm uses a Fourier-based Random feature approximation to tackle the curse of dimensionality associated with the kernel representations. Exploiting the fact that the real-world networks often exhibit sparse topologies, we propose a group lasso based optimization framework, which is solve using an iterative composite objective mirror descent method, yielding an online algorithm with fixed computational complexity per iteration. The experiments conducted on real and synthetic data show that the proposed method outperforms its competitors.
Online Non-linear Topology Identification from Graph-connected Time Series
Mar 31, 2021



Abstract:Estimating the unknown causal dependencies among graph-connected time series plays an important role in many applications, such as sensor network analysis, signal processing over cyber-physical systems, and finance engineering. Inference of such causal dependencies, often know as topology identification, is not well studied for non-linear non-stationary systems, and most of the existing methods are batch-based which are not capable of handling streaming sensor signals. In this paper, we propose an online kernel-based algorithm for topology estimation of non-linear vector autoregressive time series by solving a sparse online optimization framework using the composite objective mirror descent method. Experiments conducted on real and synthetic data sets show that the proposed algorithm outperforms the state-of-the-art methods for topology estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge