Online Hyperparameter Search Interleaved with Proximal Parameter Updates
Paper and Code
Apr 06, 2020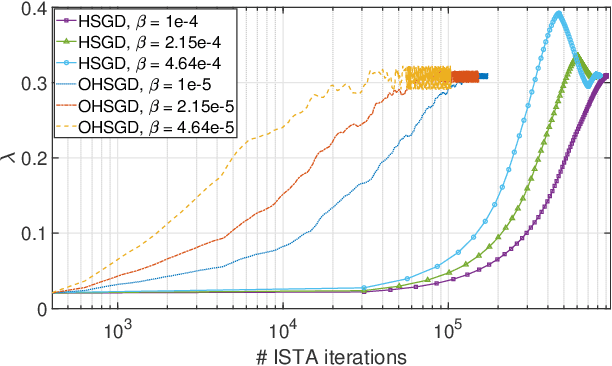
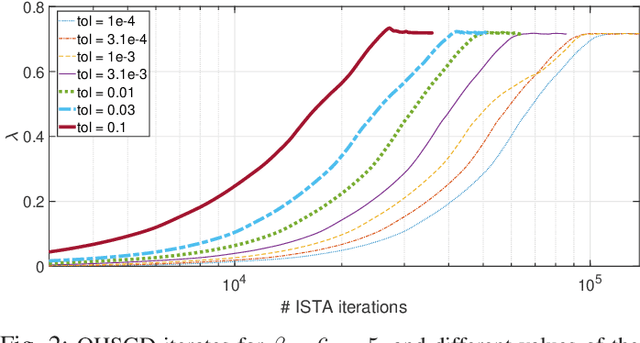
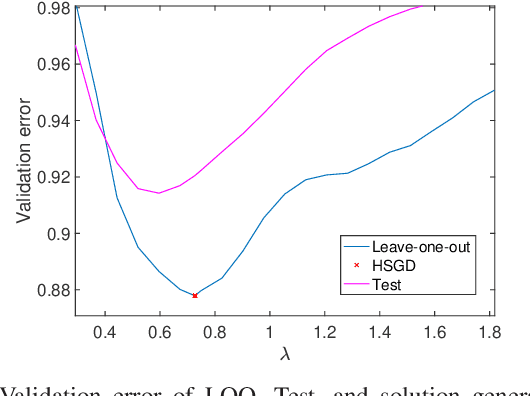
There is a clear need for efficient algorithms to tune hyperparameters for statistical learning schemes, since the commonly applied search methods (such as grid search with N-fold cross-validation) are inefficient and/or approximate. Previously existing algorithms that efficiently search for hyperparameters relying on the smoothness of the cost function cannot be applied in problems such as Lasso regression. In this contribution, we develop a hyperparameter optimization method that relies on the structure of proximal gradient methods and does not require a smooth cost function. Such a method is applied to Leave-one-out (LOO)-validated Lasso and Group Lasso to yield efficient, data-driven, hyperparameter optimization algorithms. Numerical experiments corroborate the convergence of the proposed method to a local optimum of the LOO validation error curve, and the efficiency of its approximations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge